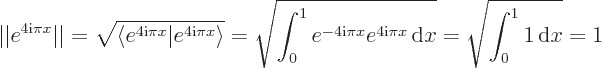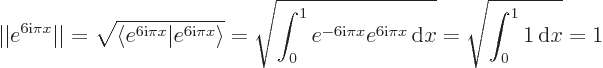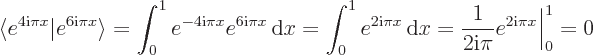| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.3.7 Solution dot-g
Question:
Show that the functions 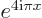 and
and 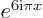 are an orthonormal set on the interval 0
are an orthonormal set on the interval 0 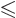
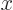
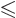 1.
1.
Answer:
You need to show that both functions are normalized, 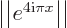
 1 and
1 and 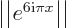
 1, and that they are mutually orthogonal,
1, and that they are mutually orthogonal, 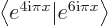
 0. Work each out in turn (don't forget to take complex conjugate of the first function in the inner products):
0. Work each out in turn (don't forget to take complex conjugate of the first function in the inner products):
(Since the Euler formula shows that 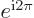
 1.)
1.)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()