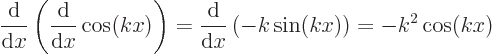| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.5.2 Solution eigvals-b
Question:
Show that any function of the form 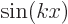 and any function of the form
and any function of the form 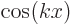 , where
, where 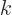 is a constant called the wave number, is an eigenfunction of the operator
is a constant called the wave number, is an eigenfunction of the operator 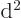
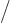
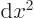 , though they are not eigenfunctions of
, though they are not eigenfunctions of 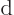
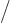
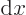 .
.
Answer:
The first derivatives are, [1, p. 60]:
so they are not eigenfunctions of 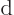
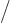
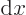 . But a second differentiation gives:
. But a second differentiation gives:
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.