| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.4.3.1 Solution esdb2-a
Question:
The 2p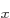 pointer state of the hydrogen atom was defined as
pointer state of the hydrogen atom was defined as
where both 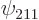 and
and 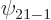 are eigenfunctions of the total energy Hamiltonian
are eigenfunctions of the total energy Hamiltonian 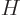 with eigenvalue
with eigenvalue 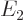 and of square angular momentum
and of square angular momentum 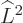 with eigenvalue
with eigenvalue 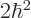 ; however,
; however, 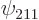 is an eigenfunction of
is an eigenfunction of 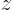 angular momentum
angular momentum 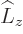 with eigenvalue
with eigenvalue 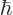 , while
, while 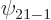 is one with eigenvalue
is one with eigenvalue 
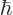 . Evaluate the expectation values of energy, square angular momentum, and
. Evaluate the expectation values of energy, square angular momentum, and 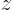 angular momentum in the 2p
angular momentum in the 2p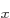 state using inner products. (Of course, since 2p
state using inner products. (Of course, since 2p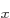 is already written out in terms of the eigenfunctions, there is no simplification in this case.)
is already written out in terms of the eigenfunctions, there is no simplification in this case.)
Answer:
For energy you have,
By the definition of eigenfunction, the products with 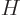 simplify:
simplify:
Multiplying out further, while noting that on account of orthonormality of the eigenstates,
you get 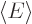

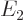 .
.
Similarly, for the square angular momentum,
or multiplying out
multiplying out further to 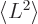

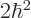 .
.
For the 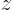 angular momentum,
angular momentum,
or multiplying out
multiplying out further to 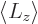
 0.
0.
![]()
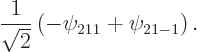
![]()