4.1.4.2 So­lu­tion harmd-b

Ques­tion:

Show that the ground state wave func­tion is max­i­mal at the ori­gin and, like all the other en­ergy eigen­func­tions, be­comes zero at large dis­tances from the ori­gin.

An­swer:

Ac­cord­ing to the an­swer to the pre­vi­ous ques­tion, the ground state is

$$\psi_{000} = {\displaystyle\frac{1}{\left(\pi\ell^2\right)^{3/4}}} e^{-r^2/2\ell^2}.$$

where $r$ is the dis­tance from the ori­gin. Now ac­cord­ing to the qual­i­ta­tive prop­er­ties of ex­po­nen­tials, an ex­po­nen­tial is one when its ar­gu­ment is zero, and be­comes less than one when its ar­gu­ment be­comes neg­a­tive. So the max­i­mum is at the ori­gin $r$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0.

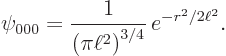
The other eigen­func­tions do not nec­es­sar­ily have their max­i­mum mag­ni­tude at the ori­gin: for ex­am­ple, the shown states $\psi_{100}$ and $\psi_{010}$ are zero at the ori­gin.

For large neg­a­tive val­ues of its ar­gu­ment, an ex­po­nen­tial be­comes very small very quickly. So if the dis­tance from the ori­gin is large com­pared to $\ell$, the wave func­tion will be neg­li­gi­ble, and it will be zero in the limit of in­fi­nite dis­tance.

For ex­am­ple, if the dis­tance from the ori­gin is just 10 times $\ell$, the ex­po­nen­tial above is al­ready as small as 0.000 000 000 002 which is clearly neg­li­gi­ble.

As far as the value of the other eigen­func­tions at large dis­tance from the ori­gin is con­cerned, note from ta­ble 4.1 that all eigen­func­tions take the generic form

$$\psi_{n_xn_yn_z} = \frac{\mbox{polynomial in $x$}}{e^{x^2/2\... ...^2/2\ell^2}} \frac{\mbox{polynomial in $z$}}{e^{z^2/2\ell^2}}.$$

For the dis­tance from the ori­gin to be­come large, at least one of $x$, $y$, or $z$ must be­come large, and then the blow up of the cor­re­spond­ing ex­po­nen­tial in the bot­tom makes the eigen­func­tions be­come zero. (What­ever the poly­no­mi­als in the top do is ir­rel­e­vant, since an ex­po­nen­tial in­cludes, ac­cord­ing to its Tay­lor se­ries, al­ways pow­ers higher than can be found in any given poly­no­mial, hence is much larger than any given poly­no­mial at large val­ues of its ar­gu­ment.)

It may be noted that the eigen­func­tions do ex­tend far­ther from the nom­i­nal po­si­tion when the en­ergy in­creases. The poly­no­mi­als get nas­tier when the en­ergy in­creases, but far enough away they must even­tu­ally al­ways lose from the ex­po­nen­tials.