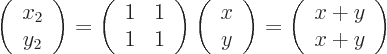| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.6.2 Solution herm-b
Question:
A matrix 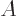 is defined to convert any vector
is defined to convert any vector 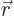

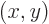 into the vector
into the vector 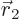

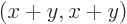 . Verify that
. Verify that 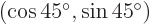 and
and 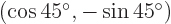 are orthonormal eigenvectors of this matrix, with eigenvalues 2 respectively 0. Note:
are orthonormal eigenvectors of this matrix, with eigenvalues 2 respectively 0. Note: 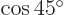

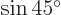

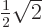 .
.
Answer:
For 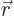

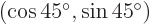

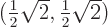 ,
, 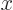

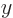

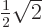 so
so 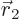

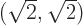 , and that is twice
, and that is twice 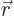 . For
. For 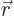

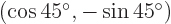

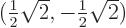 ,
, 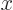

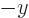

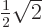 so
so 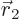
 (0,0), and that is zero times
(0,0), and that is zero times 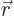 .
.
The square length of 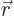

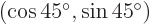 is
is 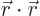 , which is given by the sum of the square components:
, which is given by the sum of the square components:  . That is one, so the vector is of length one. The same for
. That is one, so the vector is of length one. The same for 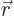

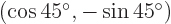 . The dot product of
. The dot product of 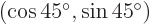 and
and 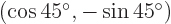 is
is 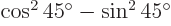 . That is zero, because
. That is zero, because 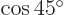

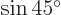 , so the two eigenvectors are orthogonal.
, so the two eigenvectors are orthogonal.
In linear algebra, you would write the relationship 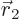

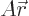 out as:
out as:
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]()