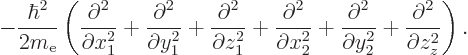5.2.1.2 So­lu­tion hmola-b

Ques­tion:

Note that the to­tal ki­netic en­ergy term is sim­ply a mul­ti­ple of the six-di­men­sion­al Lapla­cian op­er­a­tor. It treats all Carte­sian po­si­tion co­or­di­nates ex­actly the same, re­gard­less of which di­rec­tion or which elec­tron it is. Is this still the case if other par­ti­cles are in­volved?

An­swer:

The ki­netic en­ergy of the two elec­trons is

$$- \frac{\hbar^2}{2m_{\rm e}} \left( \frac{\partial^2}{\parti... ...}{\partial y_2^2} + \frac{\partial^2}{\partial z_z^2} \right).$$

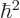
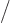
and the terms within the paren­the­ses are the six-di­men­sion­al Lapla­cian. But if other par­ti­cles would be in­volved, they would have a dif­fer­ent value of 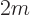$\hbar^2$$\raisebox{.5pt}{$/$}$​$2m$ and the to­tal op­er­a­tor would no longer be the nor­mal Lapla­cian.

All else be­ing the same, heav­ier par­ti­cles would have less ki­netic en­ergy. But, of course, all else is usu­ally not the same. For ex­am­ple, the atoms in no­ble gases have the same ki­netic en­ergy at the same tem­per­a­ture re­gard­less of atom mass.