| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
5.2.3.1 Solution hmolc-a
Question:
Suppose, given the wave function 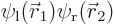 , that you found an electron near the left proton. What electron would it probably be? Suppose you found an electron at the point halfway in between the protons. What electron would that likely be?
, that you found an electron near the left proton. What electron would it probably be? Suppose you found an electron at the point halfway in between the protons. What electron would that likely be?
Answer:
The total probability of finding electron 1 at a position 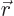 is
is
since 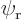 is normalized. Similarly, the probability of finding electron 2 at position
is normalized. Similarly, the probability of finding electron 2 at position 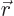 is
is 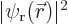 .
.
If 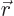 is close to the left proton,
is close to the left proton, 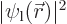 is significant, but
is significant, but 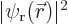 is small, so you are much more likely to find electron 1 there than electron 2.
is small, so you are much more likely to find electron 1 there than electron 2.
But at the point halfway in between the protons, 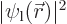 and
and 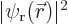 are equal by symmetry, and you are just as likely to find electron 1 there as electron 2.
are equal by symmetry, and you are just as likely to find electron 1 there as electron 2.
![]() ,
,![]()
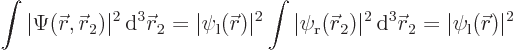
![]()
![]()
![]()
![]()
![]()