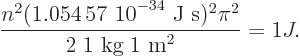3.5.6.3 So­lu­tion pipee-c

Ques­tion:

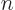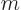
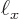
What is the eigen­func­tion num­ber, or quan­tum num­ber, $n$ that pro­duces a macro­scopic amount of en­ergy, 1 J, for macro­scopic val­ues $m$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1 kg and $\ell_x$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1 m? With that many en­ergy lev­els in­volved, would you see the dif­fer­ence be­tween suc­ces­sive ones?

An­swer:

Putting the generic ex­pres­sion for the eigen­val­ues,

$$E_n = \frac{n^2\hbar^2\pi^2}{2m\ell_x^2}$$

equal to 1 J and plug­ging in the given num­bers:

$$\frac{n^2(\mbox{1.054 57 10$\POW9,{-34}$ J s})^2\pi^2} {2\;\mbox{1 kg}\;\mbox{1 m}^2} = 1 J.$$

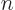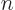
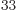Solv­ing for $n$, you get $n$ $\vphantom0\raisebox{1.5pt}{$=$}$ 4.268 64 10$\POW9,{33}$. Ob­vi­ously, there is no way to dis­tin­guish that many en­ergy lev­els. A cal­cu­la­tor can­not even dis­play all 34 dig­its of this num­ber, even if you knew 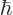$\hbar$ to enough dig­its ac­cu­racy to com­pute 34 dig­its.