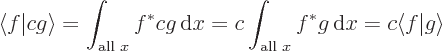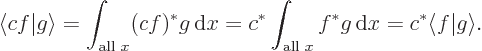2.6.4 So­lu­tion herm-d

Ques­tion:

Gen­er­al­ize the pre­vi­ous ques­tion, by show­ing that any com­plex con­stant 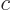$c$ comes out of the right hand side of an in­ner prod­uct un­changed, but out of the left hand side as its com­plex con­ju­gate;

$$\langle f\vert cg\rangle = c \langle f\vert g\rangle\qquad\langle c f\vert g\rangle = c^* \langle f\vert g\rangle .$$

As a re­sult, a num­ber 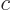$c$ is only a Her­mit­ian op­er­a­tor if it is real: if 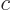$c$ is com­plex, the two ex­pres­sions above are not the same.

An­swer:

Since con­stants can be taken out of an in­te­gral:

$$\langle f\vert c g\rangle = \int_{\mbox{\scriptsize all }x} ... ...scriptsize all }x} f^* g{ \rm d}x = c \langle f\vert g\rangle$$

$$\langle cf\vert g\rangle = \int_{\mbox{\scriptsize all }x} (... ...ptsize all }x} f^* g{ \rm d}x = c^* \langle f\vert g\rangle .$$