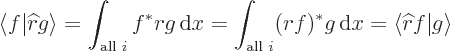| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.6.5 Solution herm-e
Question:
Show that an operator such as 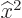 , corresponding to multiplying by a real function, is an Hermitian operator.
, corresponding to multiplying by a real function, is an Hermitian operator.
Answer:
If the operator corresponds to multiplying by a real function of 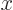 , call it
, call it 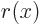 , then
, then
since the complex conjugate does not affect a real function.
![]() ,
,![]() ,
,![]() ,
,