| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.6.6 Solution herm-f
Question:
Show that the operator 

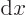 is not a Hermitian operator, but
is not a Hermitian operator, but 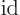

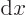 is, assuming that the functions on which they act vanish at the ends of the interval
is, assuming that the functions on which they act vanish at the ends of the interval 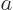

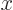

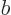 on which they are defined. (Less restrictively, it is only required that the functions are
on which they are defined. (Less restrictively, it is only required that the functions are periodic
; they must return to the same value at 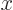

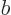 that they had at
that they had at 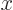

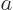 .)
.)
Answer:
You first need to show that
is not the same as
in order for 

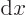 not to be a Hermitian operator.
not to be a Hermitian operator.
By definition,
You can use integration by parts,
[1, p. 64], to move the derivative from 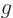 to
to 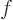 :
:
(the differentiation can be moved inside the complex conjugate since it is a real operation.) Since the functions 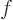 and
and 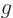 are the same at the end points
are the same at the end points 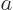 and
and 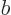 you have
you have
This makes 

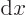 a skew-Hermitian operator, rather than a Hermitian one: flipping over the operator to the other side changes the sign of the inner product.
a skew-Hermitian operator, rather than a Hermitian one: flipping over the operator to the other side changes the sign of the inner product.
To get rid of the change of sign, you can add a factor 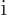 to the operator, since the
to the operator, since the 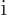 adds a compensating minus sign when you bring it inside the complex conjugate:
adds a compensating minus sign when you bring it inside the complex conjugate:
This makes 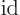

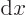 a Hermitian operator.
a Hermitian operator.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.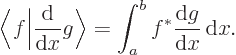

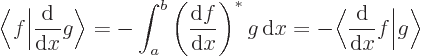
![]()
![]()