| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.6.8 Solution herm-h
Question:
A complete set of orthonormal eigenfunctions of 
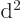

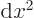 on the interval 0
on the interval 0 
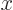

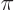 that are zero at the end points is the infinite set of functions
that are zero at the end points is the infinite set of functions
Check that these functions are indeed zero at 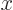
 0 and
0 and 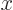

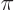 , that they are indeed orthonormal, and that they are eigenfunctions of
, that they are indeed orthonormal, and that they are eigenfunctions of 
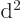

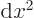 with the positive real eigenvalues
with the positive real eigenvalues
Completeness is a much more difficult thing to prove, but they are. The completeness proof in the notes covers this case.
Answer:
Any eigenfunction of the above list can be written in the generic form 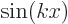

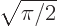 where
where 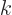 is a positive whole number, in other words where
is a positive whole number, in other words where 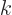 is a
is a natural
number (one of 1, 2, 3, 4, ....) If you show that the stated properties are true for this generic form, it means that they are true for every eigenfunction.
First check the end points. The graph of the sine function, [1, item 12.22], shows that a sine is zero whenever its argument is a whole multiple of 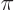 . That makes both
. That makes both 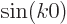

 and
and 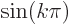 zero. So
zero. So 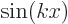

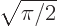 must be zero at
must be zero at 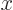
 0 and
0 and 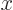

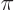 too.
too.
Now check that the norm of the eigenfunctions is one. First find the norm of 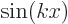 by itself:
by itself:
Since the sine is real, the complex conjugate does not do anything, and you get
using [1, item 18.26]. Dividing this by 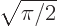 , the norm
, the norm 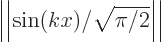 becomes one; every eigenfunction is normalized.
becomes one; every eigenfunction is normalized.
To verify that 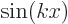

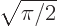 is orthogonal to every other eigenfunction, take the generic other eigenfunction to be
is orthogonal to every other eigenfunction, take the generic other eigenfunction to be 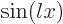

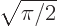 with
with  a natural number different from
a natural number different from 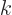 . You must then show that the inner product of these two eigenfunctions is zero. Since the normalization constants do not make any difference here, you can just show that
. You must then show that the inner product of these two eigenfunctions is zero. Since the normalization constants do not make any difference here, you can just show that  is zero. You get
is zero. You get
using again [1, item 18.26].
Ahem. Completeness. Well, just don't worry about it. There are a heck of a lot of functions here. Infinitely many of them, to be precise. Surely, with infinitely many functions, you should be able to approximate any given function to good accuracy?
(This statement is, of course, deliberately ludicrous. In fact, if you leave out a single eigenfunction, say the 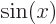 function, the remaining infinitely many functions
function, the remaining infinitely many functions 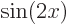 ,
, 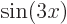 , ...can simply not reproduce it by themselves. The best they can do is being zero and not try to approximate
, ...can simply not reproduce it by themselves. The best they can do is being zero and not try to approximate 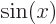 at all. Still, if you do include
at all. Still, if you do include 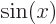 in the sequence, any (reasonable) function can be described accurately by a combination of the sines. It was hard to prove initially; in fact, Fourier in his thesis did not. The first proof is due to Dirichlet.)
in the sequence, any (reasonable) function can be described accurately by a combination of the sines. It was hard to prove initially; in fact, Fourier in his thesis did not. The first proof is due to Dirichlet.)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
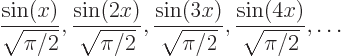
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()

![]()
![]() ,
,![]() ,
,![]()
![]()