| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.6.9 Solution herm-i
Question:
A complete set of orthonormal eigenfunctions of the operator 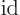

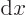 that are periodic on the interval 0
that are periodic on the interval 0 
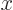

 are the infinite set of functions
are the infinite set of functions
Check that these functions are indeed periodic, orthonormal, and that they are eigenfunctions of 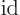

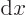 with the real eigenvalues
with the real eigenvalues
Completeness is a much more difficult thing to prove, but they are. The completeness proof in the notes covers this case.
Answer:
Any eigenfunction of the above list can be written in the generic form 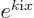

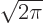 where
where 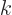 is a whole number, in other words where
is a whole number, in other words where 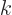 is an integer, one of ...,
is an integer, one of ...,  3,
3,  2,
2,  1, 0, 1, 2, 3, ... If you show that the stated properties are true for this generic form, it means that they are true for every eigenfunction.
1, 0, 1, 2, 3, ... If you show that the stated properties are true for this generic form, it means that they are true for every eigenfunction.
Now periodicity requires that 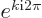

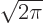

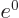

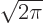 , and the Euler formula verifies this: sines and cosines are the same if the angle changes by a whole multiple of
, and the Euler formula verifies this: sines and cosines are the same if the angle changes by a whole multiple of  . (For example,
. (For example,  ,
, 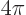 ,
, 
 , etcetera are physically all equivalent to a zero angle.)
, etcetera are physically all equivalent to a zero angle.)
The derivative of 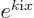

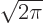 with respect to
with respect to 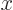 is
is 

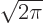 , and multiplying by
, and multiplying by 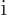 you get
you get 
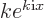

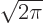 , so
, so 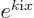

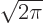 is an eigenfunction of
is an eigenfunction of 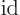

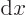 with eigenvalue
with eigenvalue 
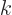 .
.
To see that 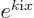

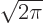 is normalized, check that its norm is unity:
is normalized, check that its norm is unity:
To verify that 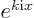

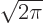 is orthogonal to every other eigenfunction, take the generic other eigenfunction to be
is orthogonal to every other eigenfunction, take the generic other eigenfunction to be 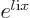

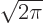 with
with  an integer different from
an integer different from 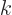 . You must then show that the inner product of these two eigenfunctions is zero. Since the normalization constants do not make any difference here, you can just show that
. You must then show that the inner product of these two eigenfunctions is zero. Since the normalization constants do not make any difference here, you can just show that  is zero. You get
is zero. You get
since 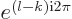

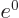
 1. So different eigenfunctions are orthogonal, their inner product is zero.
1. So different eigenfunctions are orthogonal, their inner product is zero.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
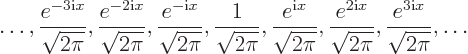
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 3
3![]() 2
2![]() 1
1![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() .
.![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
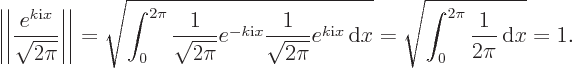
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()