6.10 Fermi En­ergy of the Free-Elec­tron Gas

As the pre­vi­ous sec­tion dis­cussed, a sys­tem of non­in­ter­act­ing elec­trons, a free-elec­tron gas, oc­cu­pies a range of sin­gle-par­ti­cle en­er­gies. Now the elec­trons with the high­est sin­gle-par­ti­cle en­er­gies are par­tic­u­larly im­por­tant. The rea­son is that these elec­trons have empty sin­gle-par­ti­cle states avail­able at just very slightly higher en­ergy. There­fore, these elec­trons are eas­ily ex­cited to do use­ful things, like con­duct elec­tric­ity for ex­am­ple. In con­trast, elec­trons in en­ergy states of lower en­ergy do not have empty states within easy reach. There­fore lower en­ergy elec­tron are es­sen­tially stuck in their states; they do not usu­ally con­tribute to non­triv­ial elec­tronic ef­fects.

Va­lence elec­trons in met­als be­have qual­i­ta­tively much like a free-elec­tron gas. For them too, the elec­trons in the high­est en­ergy sin­gle-par­ti­cle states are the crit­i­cal ones for the metal­lic prop­er­ties. There­fore, the high­est sin­gle-par­ti­cle en­ergy oc­cu­pied by elec­trons in the sys­tem ground state has been given a spe­cial name; the Fermi en­ergy. In the en­ergy spec­trum of the free-elec­tron gas to the right in fig­ure 6.11, the Fermi en­ergy is in­di­cated by a red tick mark on the axis.

Also, the sur­face that the elec­trons of high­est en­ergy oc­cupy in wave num­ber space is called the Fermi sur­face. For the free-elec­tron gas the wave num­ber space was il­lus­trated to the left in fig­ure 6.11. The Fermi sur­face is out­lined in red in the fig­ure; it is the spher­i­cal out­side sur­face of the oc­cu­pied re­gion.

One is­sue that is im­por­tant for un­der­stand­ing the prop­er­ties of sys­tems of elec­trons is the over­all mag­ni­tude of the Fermi en­ergy. Re­call first that for a sys­tem of bosons, in the ground state all bosons are in the sin­gle-par­ti­cle state of low­est en­ergy. That state cor­re­sponds to the point clos­est to the ori­gin in wave num­ber space. It has very lit­tle en­ergy, even in terms of atomic units of elec­tronic en­ergy. That was il­lus­trated nu­mer­i­cally in ta­ble 6.1. The low­est sin­gle-par­ti­cle en­ergy is, as­sum­ing that the box is cu­bic

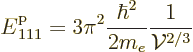$${\vphantom' E}^{\rm p}_{111} = 3\pi^2 \frac{\hbar^2}{2m_e} \frac{1}{{\cal V}^{2/3}}$$ (6.15)

where $m_{\rm e}$ is the elec­tron mass and ${\cal V}$ the vol­ume of the box.

Un­like for bosons, for elec­trons only two elec­trons can go into the low­est en­ergy state. Or in any other spa­tial state for that mat­ter. And since a macro­scopic sys­tem has a gi­gan­tic num­ber of elec­trons, it fol­lows that a gi­gan­tic num­ber of states must be oc­cu­pied in wave num­ber space. There­fore the states on the Fermi sur­face in fig­ure 6.11 are many or­ders of mag­ni­tude fur­ther away from the ori­gin than the state of low­est en­ergy. And since the en­ergy is pro­por­tional to the square dis­tance from the ori­gin, that means that the Fermi en­ergy is many or­ders of mag­ni­tude larger than the low­est sin­gle-par­ti­cle en­ergy ${\vphantom' E}^{\rm p}_{111}$.

More pre­cisely, the Fermi en­ergy of a free-elec­tron gas can be ex­pressed in terms of the num­ber of elec­trons per unit vol­ume $I$$\raisebox{.5pt}{$/$}$​${\cal V}$ as:

$$\fbox{$\displaystyle {\vphantom' E}^{\rm p}_{\rm{F}} = \le... ...ac{\hbar^2}{2m_e} \left(\frac{I}{{\cal V}}\right)^{2/3} $} %$$ (6.16)

To check this re­la­tion­ship, in­te­grate the den­sity of states (6.6) given in sec­tion 6.3 from zero to the Fermi en­ergy. That gives the to­tal num­ber of oc­cu­pied states, which equals the num­ber of elec­trons $I$. In­vert­ing the ex­pres­sion to give the Fermi en­ergy in terms of $I$ pro­duces the re­sult above.

It fol­lows that the Fermi en­ergy is larger than the low­est sin­gle-par­ti­cle en­ergy by the gi­gan­tic fac­tor

$$\frac{I^{2/3}}{\left(3\pi^2\right)^{1/3}}$$

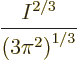
It is in­struc­tive to put some ball­park num­ber to the Fermi en­ergy. In par­tic­u­lar, take the va­lence elec­trons in a block of cop­per as a model. As­sum­ing one va­lence elec­tron per atom, the elec­tron den­sity $I$$\raisebox{.5pt}{$/$}$​${\cal V}$ in the ex­pres­sion for the Fermi en­ergy equals the atom den­sity. That can be es­ti­mated to be 8.5 10$\POW9,{28}$ atoms/m$\POW9,{3}$ by di­vid­ing the mass den­sity, 9 000 kg/m$\POW9,{3}$, by the mo­lar mass, 63.5 kg/kmol, and then mul­ti­ply­ing that by Avo­gadro’s num­ber, 6.02 10$\POW9,{26}$ par­ti­cles/kmol. Plug­ging it in (6.16) then gives a Fermi en­ergy of 7 eV (elec­tron Volt). That is quite a lot of en­ergy, about half the 13.6 eV ion­iza­tion en­ergy of hy­dro­gen atoms.

The Fermi en­ergy gives the max­i­mum en­ergy that an elec­tron can have. The av­er­age en­ergy that they have is com­pa­ra­ble but some­what smaller:

$${\vphantom' E}^{\rm p}_{\rm average} = {\textstyle\frac{3}{5}} {\vphantom' E}^{\rm p}_{\rm {F}}$$ (6.17)

To ver­ify this ex­pres­sion, find the to­tal en­ergy $E$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\int{\vphantom' E}^{\rm p}{\cal V}{\cal D}{\,\rm d}{\vphantom' E}^{\rm p}$ of the elec­trons us­ing (6.6) and di­vide by the num­ber of elec­trons $I$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\int{\cal V}{\cal D}{\,\rm d}{\vphantom' E}^{\rm p}$. The in­te­gra­tion is again over the oc­cu­pied states, so from zero to the Fermi en­ergy.

For cop­per, the ball­park av­er­age en­ergy is 4.2 eV. To put that in con­text, con­sider the equiv­a­lent tem­per­a­ture at which clas­si­cal par­ti­cles would need to be to have the same av­er­age ki­netic en­ergy. Mul­ti­ply­ing 4.2 eV by $e$$\raisebox{.5pt}{$/$}$​$\frac32k_{\rm B}$ gives an equiv­a­lent tem­per­a­ture of 33 000 K. That is gi­gan­tic even com­pared to the melt­ing point of cop­per, 1 356 K. It is all due to the ex­clu­sion prin­ci­ple that pre­vents the elec­trons from drop­ping down into the al­ready filled states of lower en­ergy.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The Fermi en­ergy is the high­est sin­gle-par­ti­cle en­ergy that a sys­tem of elec­trons at ab­solute zero tem­per­a­ture will oc­cupy.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

It is nor­mally a very high en­ergy.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The Fermi sur­face is the sur­face that the elec­trons with the Fermi en­ergy oc­cupy in wave num­ber space.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The av­er­age en­ergy per elec­tron for a free-elec­tron gas is 60% of the Fermi en­ergy.