8.5 Fail­ure of the Schrö­din­ger Equa­tion?

Sec­tion {8.2} men­tioned send­ing half of the wave func­tion of an elec­tron to Venus, and half to Mars. A scat­ter­ing setup as de­scribed in chap­ter 7.12 pro­vides a prac­ti­cal means for ac­tu­ally do­ing this, (at least, for tak­ing the wave func­tion apart in two sep­a­rate parts.) The ob­vi­ous ques­tion is now: can the Schrö­din­ger equa­tion also de­scribe the phys­i­cally ob­served col­lapse of the wave func­tion, where the elec­tron changes from be­ing on both Venus and Mars with a 50/50 prob­a­bil­ity to, say, be­ing on Mars with ab­solute cer­tainty?

The an­swer ob­tained in this and the next sub­sec­tion will be most cu­ri­ous: no, the Schrö­din­ger equa­tion flatly con­tra­dicts that the wave func­tion col­lapses, but yes, it re­quires that mea­sure­ment leads to the ex­per­i­men­tally ob­served col­lapse. The analy­sis will take us to a mind-bog­gling but re­ally un­avoid­able con­clu­sion about the very na­ture of our uni­verse.

This sub­sec­tion will ex­am­ine the prob­lem the Schrö­din­ger equa­tion has with de­scrib­ing a col­lapse. First of all, the so­lu­tions of the lin­ear Schrö­din­ger equa­tion do not al­low a math­e­mat­i­cally ex­act col­lapse like some non­lin­ear equa­tions do. But that does not nec­es­sar­ily im­ply that so­lu­tions would not be able to col­lapse phys­i­cally. It would be con­ceiv­able that the so­lu­tion could evolve to a state where the elec­tron is on Mars with such high prob­a­bil­ity that it can be taken to be cer­tainty. In fact, a com­mon no­tion is that, some­how, in­ter­ac­tion with a macro­scopic mea­sure­ment ap­pa­ra­tus could lead to such an end re­sult.

Of course, the con­stituent par­ti­cles that make up such a macro­scopic mea­sure­ment ap­pa­ra­tus still need to sat­isfy the laws of physics. So let’s make up a rea­son­able model for such a com­plete macro­scopic sys­tem, and see what can then be said about the pos­si­bil­ity for the wave func­tion to evolve to­wards the elec­tron be­ing on Mars.

The model will ig­nore the ex­is­tence of any­thing be­yond the Venus, Earth, Mars sys­tem. It will be as­sumed that the three plan­ets con­sist of a hu­mon­gous, but fi­nite, num­ber of con­served clas­si­cal par­ti­cles $1,2,3,4,5,\ldots$, with a su­per­colos­sal wave func­tion:

$$\Psi({\skew0\vec r}_1, S_{z1}, {\skew0\vec r}_2, S_{z2}, {... ...}, {\skew0\vec r}_4, S_{z4}, {\skew0\vec r}_5, S_{z5}, \ldots)$$

Par­ti­cle 1 will be taken to be the scat­tered elec­tron. It will be as­sumed that the wave func­tion sat­is­fies the Schrö­din­ger equa­tion:

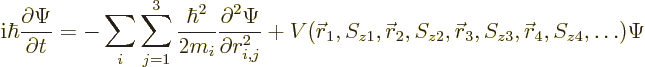$${\rm i}\hbar \frac{\partial\Psi}{\partial t} = - \sum_i \s... ...skew0\vec r}_3, S_{z3}, {\skew0\vec r}_4, S_{z4}, \ldots) \Psi$$ (8.1)

Try­ing to write the so­lu­tion to this prob­lem would of course be pro­hib­i­tive, but the evo­lu­tion of the prob­a­bil­ity of the elec­tron to be on Venus can still be ex­tracted from it with some fairly stan­dard ma­nip­u­la­tions. First, tak­ing the com­bi­na­tion of the Schrö­din­ger equa­tion times $\Psi^*$ mi­nus the com­plex con­ju­gate of the Schrö­din­ger equa­tion times $\Psi$ pro­duces af­ter some fur­ther ma­nip­u­la­tion an equa­tion for the time de­riv­a­tive of the prob­a­bil­ity:

$${\rm i}\hbar \frac{\partial\Psi^*\Psi}{\partial t} = - \su... ...i,j}} - \Psi \frac{\partial\Psi^*}{\partial r_{i,j}} \right)$$ (8.2)

The ques­tion is the prob­a­bil­ity for the elec­tron to be on Venus, and you can get that by in­te­grat­ing the prob­a­bil­ity equa­tion above over all pos­si­ble po­si­tions and spins of the par­ti­cles ex­cept for par­ti­cle 1, for which you have to re­strict the spa­tial in­te­gra­tion to Venus and its im­me­di­ate sur­round­ings. If you do that, the left hand side be­comes the rate of change of the prob­a­bil­ity for the elec­tron to be on Venus, re­gard­less of the po­si­tion and spin of all the other par­ti­cles.

In­ter­est­ingly, as­sum­ing times at which the Venus part of the scat­tered elec­tron wave is def­i­nitely at Venus, the right hand side in­te­grates to zero: the wave func­tion is sup­posed to dis­ap­pear at large dis­tances from this iso­lated sys­tem, and when­ever par­ti­cle 1 would be at the bor­der of the sur­round­ings of Venus.

It fol­lows that the prob­a­bil­ity for the elec­tron to be at Venus can­not change from 50%. A true col­lapse of the wave func­tion of the elec­tron as pos­tu­lated in the or­tho­dox in­ter­pre­ta­tion, where the prob­a­bil­ity to find the elec­tron at Venus changes to 100% or 0% can­not oc­cur.

Of course, the model was sim­ple; you might there­fore con­jec­ture that a true col­lapse could oc­cur if ad­di­tional physics is in­cluded, such as non­con­served par­ti­cles like pho­tons, or other rel­a­tivis­tic ef­fects. But that would ob­vi­ously be a mov­ing tar­get. The analy­sis made a good-faith ef­fort to ex­am­ine whether in­clud­ing macro­scopic ef­fects may cause the ob­served col­lapse of the wave func­tion, and the an­swer was no. Hav­ing a sci­en­tif­i­cally open mind re­quires you to at least fol­low the model to its log­i­cal end; na­ture might be telling you some­thing here.

Is it re­ally true that the re­sults dis­agree with the ob­served physics? You need to be care­ful. There is no rea­son­able doubt that if a mea­sure­ment is per­formed about the pres­ence of the elec­tron on Venus, the wave func­tion will be ob­served to col­lapse. But all you es­tab­lished above is that the wave func­tion does not col­lapse; you did not es­tab­lish whether or not it will be ob­served to col­lapse. To an­swer the ques­tion whether a col­lapse will be ob­served, you will need to in­clude the ob­servers in your rea­son­ing.

The prob­lem is with the in­nocu­ous look­ing phrase re­gard­less of the po­si­tion and spin of all the other par­ti­cles in the ar­gu­ments above. Even while the to­tal prob­a­bil­ity for the elec­tron to be at Venus must stay at 50% in this ex­am­ple sys­tem, it is still per­fectly pos­si­ble for the prob­a­bil­ity to be­come 100% for one state of the par­ti­cles that make up the ob­server and her tools, and to be 0% for an­other state of the ob­server and her tools.

It is per­fectly pos­si­ble to have a state of the ob­server with brain par­ti­cles, ink-on-pa­per par­ti­cles, tape recorder par­ti­cles, that all say that the elec­tron is on Venus, com­bined with 100% prob­a­bil­ity that the elec­tron is on Venus, and a sec­ond state of the ob­server with brain par­ti­cles, ink-on-pa­per par­ti­cles, tape recorder par­ti­cles, that all say the elec­tron must be on Mars, com­bined with 0% prob­a­bil­ity for the elec­tron to be on Venus. Such a sce­nario is called a “rel­a­tive state in­ter­pre­ta­tion;” the states of the ob­server and the mea­sured ob­ject be­come en­tan­gled with each other.

The state of the elec­tron does not change to a sin­gle state of pres­ence or ab­sence; in­stead two states of the macro­scopic uni­verse de­velop, one with the elec­tron ab­sent, the other with it present. As ex­plained in the next sub­sec­tion, the Schrö­din­ger equa­tion does not just al­low this to oc­cur, it re­quires this to oc­cur. So, far from be­ing in con­flict with the ob­served col­lapse, the model above re­quires it. The model pro­duces the right physics: ob­served col­lapse is a con­se­quence of the Schrö­din­ger equa­tion, not of some­thing else.

But all this ends up with the rather dis­turb­ing thought that there are now two states of the uni­verse, and the two are dif­fer­ent in what they think about the elec­tron. This con­clu­sion was un­ex­pected; it comes as the un­avoid­able con­se­quence of the math­e­mat­i­cal equa­tions that quan­tum me­chan­ics ab­stracted for the way na­ture op­er­ates.