| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
2.1 Complex Numbers
Quantum mechanics is full of complex numbers, numbers involving
Note that  is not an ordinary,
is not an ordinary, real
,
number, since there is no real number whose square is  1; the square
of a real number is always positive. This section summarizes the
most important properties of complex numbers.
1; the square
of a real number is always positive. This section summarizes the
most important properties of complex numbers.
First, any complex number, call it  , can by definition always
be written in the form
, can by definition always
be written in the form
 |
(2.1) |
where both 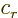 and
and 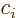 are ordinary real numbers, not involving
are ordinary real numbers, not involving
 . The number
. The number 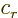 is called the real part of
is called the real part of  and
and 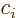 the imaginary part.
the imaginary part.
You can think of the real and imaginary parts of a complex number
as the components of a two-dimensional vector:
The length of that vector is called the “magnitude,” or “absolute value”  of the complex number. It equals
of the complex number. It equals
Complex numbers can be manipulated pretty much in the same way as
ordinary numbers can. A relation to remember is:
 |
(2.2) |
which can be verified by multiplying the top and bottom of the
fraction by  and noting that by definition
and noting that by definition 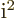

 1 in the
bottom.
1 in the
bottom.
The complex conjugate of a complex number  , denoted by
, denoted by
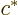 , is found by replacing
, is found by replacing  everywhere by
everywhere by 
 .
In particular, if
.
In particular, if 

 , where
, where 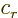 and
and
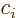 are real numbers, the complex conjugate is
are real numbers, the complex conjugate is
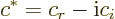 |
(2.3) |
The following picture shows that graphically, you get the complex
conjugate of a complex number by flipping it over around the
horizontal axis:
You can get the magnitude of a complex number  by multiplying
by multiplying  with its complex conjugate
with its complex conjugate 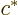 and taking a square root:
and taking a square root:
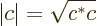 |
(2.4) |
If 

 , where
, where 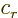 and
and 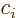 are real
numbers, multiplying out
are real
numbers, multiplying out 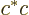 shows the magnitude of
shows the magnitude of  to be
to be
which is indeed the same as before.
From the above graph of the vector representing a complex number
 , the real part is
, the real part is 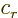

 where
where  is the angle that the vector makes with the horizontal axis, and the
imaginary part is
is the angle that the vector makes with the horizontal axis, and the
imaginary part is 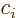

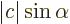 . So you can write
any complex number in the form
. So you can write
any complex number in the form
The critically important Euler formula says that:
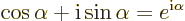 |
(2.5) |
So, any complex number can be written in polar form
as
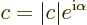 |
(2.6) |
where both the magnitude  and the phase angle (or argument)
and the phase angle (or argument)
 are real numbers.
are real numbers.
Any complex number of magnitude one can therefore be written as
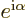 . Note that the only two real numbers of
magnitude one, 1 and
. Note that the only two real numbers of
magnitude one, 1 and  1, are included for
1, are included for 
 0,
respectively
0,
respectively 

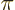 . The number
. The number  is obtained
for
is obtained
for 

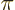
 2 and
2 and 
 for
for 


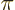
 2.
2.
(See derivation {D.7} if you want to know where the Euler
formula comes from.)
Key Points

- Complex numbers include the square root of minus one,
 , as a valid number.
, as a valid number.

- All complex numbers can be written as a real part plus
 times an imaginary part, where both parts are normal real numbers.
times an imaginary part, where both parts are normal real numbers.

- The complex conjugate of a complex number is obtained by
replacing
 everywhere by
everywhere by 
 .
.

- The magnitude of a complex number is obtained by multiplying the
number by its complex conjugate and then taking a square root.

- The Euler formula relates exponentials to sines and cosines.
2.1 Review Questions
-
1.
-
Multiply out 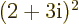 and then find its real and imaginary part.
and then find its real and imaginary part.
Solution mathcplx-a
-
2.
-
Show more directly that 1



 .
.
Solution mathcplx-b
-
3.
-
Multiply out 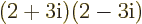 and then find its real and imaginary part.
and then find its real and imaginary part.
Solution mathcplx-c
-
4.
-
Find the magnitude or absolute value of  .
.
Solution mathcplx-d
-
5.
-
Verify that  is still the complex conjugate of
is still the complex conjugate of 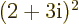 if both are multiplied out.
if both are multiplied out.
Solution mathcplx-e
-
6.
-
Verify that 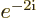 is still the complex conjugate of
is still the complex conjugate of 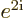 after both are rewritten using the Euler formula.
after both are rewritten using the Euler formula.
Solution mathcplx-f
-
7.
-
Verify that 
 2
2 
 .
.
Solution mathcplx-g
-
8.
-
Verify that 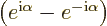

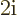

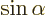 .
.
Solution mathcplx-h
![]() ,
,![\begin{displaymath}
\begin{picture}(200,70)(-100,-20)
\thinlines
\put(-50,0...
...tor(2,1){70}}
\put(0,23){\makebox(0,0)[tl]{$c$}}
\end{picture}\end{displaymath}](img187.gif)
![]() ,
,![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![\begin{displaymath}
\begin{picture}(200,100)(-100,-50)
\thinlines
\put(-50,...
...2,-1){70}}
\put(0,-23){\makebox(0,0)[bl]{$c^*$}}
\end{picture}\end{displaymath}](img194.gif)
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() .
.![]() 1
1![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
,
.
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.