| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
N.11 Better description of two-state systems
An approximate definition of the states  and
and  would
make the states
would
make the states  and
and  only approximate
energy eigenstates. But they can be made exact energy eigenfunctions
by defining
only approximate
energy eigenstates. But they can be made exact energy eigenfunctions
by defining 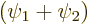

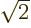 and
and 

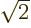 to
be the exact symmetric ground state and the exact antisymmetric state
of second lowest energy. The precise
to
be the exact symmetric ground state and the exact antisymmetric state
of second lowest energy. The precise basic
wave
function  and
and  can then be reconstructed from that.
can then be reconstructed from that.
Note that  and
and  themselves are not energy eigenstates,
though they might be so by approximation. The errors in this
approximation, even if small, will produce the wrong result for the
time evolution. (The small differences in energy drive the
nontrivial part of the unsteady evolution.)
themselves are not energy eigenstates,
though they might be so by approximation. The errors in this
approximation, even if small, will produce the wrong result for the
time evolution. (The small differences in energy drive the
nontrivial part of the unsteady evolution.)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()