| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.35 The evolution of expectation values
To verify the stated formulae for the evolution of expectation values,
just write the definition of expectation value,
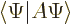 , differentiate to get
, differentiate to get
and replace 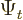 by
by 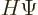
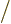
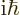 on account of the Schrödinger
equation. Note that in the first inner product, the
on account of the Schrödinger
equation. Note that in the first inner product, the 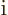 appears in
the left part, hence comes out as its complex conjugate
appears in
the left part, hence comes out as its complex conjugate 
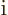 .
.
![]() ,
,