| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.76 Harmonic oscillator revisited
This note rederives the harmonic oscillator solution, but in spherical
coordinates. The reason to do so is to obtain energy eigenfunctions
that are also eigenfunctions of square angular momentum and of angular
momentum in the  -direction. The derivation is very similar to the
one for the hydrogen atom given in derivation {D.15},
so the discussion will mainly focus on the differences.
-direction. The derivation is very similar to the
one for the hydrogen atom given in derivation {D.15},
so the discussion will mainly focus on the differences.
The solutions are again in the form 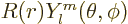 with the
with the
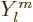 the spherical harmonics. However, the radial functions
the spherical harmonics. However, the radial functions  are different; the equation for them is now
are different; the equation for them is now
The difference from {D.15} is that a harmonic
oscillator potential  has replaced the Coulomb
potential. A suitable rescaling is now
has replaced the Coulomb
potential. A suitable rescaling is now 

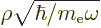 , which produces
, which produces
where 



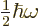 is the energy in half quanta.
is the energy in half quanta.
Split off the expected asymptotic behavior for large 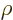 by defining
by defining
Then  satisfies
satisfies
Plug in a power series 

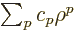 , then the
coefficients must satisfy:
, then the
coefficients must satisfy:
From that it is seen that the lowest power in the series is


 ,
, 

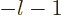 not being
acceptable. Also the series must terminate, or blow up will occur.
That requires that
not being
acceptable. Also the series must terminate, or blow up will occur.
That requires that 

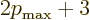 . So the
energy must be
. So the
energy must be 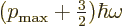 with
with  an integer no smaller than
an integer no smaller than  , so at least zero.
, so at least zero.
Therefore, numbering the energy levels from 
 1 like for the hydrogen
level gives the energy levels as
1 like for the hydrogen
level gives the energy levels as
That are the same energy levels as derived in Cartesian coordinates,
as they should be. However, the eigenfunctions are different. They
are of the form
where 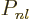 is some polynomial of degree
is some polynomial of degree  , whose lowest
power of
, whose lowest
power of 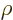 is
is  . The value of the azimuthal quantum
number
. The value of the azimuthal quantum
number  must run up to
must run up to  like for the hydrogen atom. However,
in this case
like for the hydrogen atom. However,
in this case  must be odd or even depending on whether
must be odd or even depending on whether  is odd
or even, or the power series will not terminate.
is odd
or even, or the power series will not terminate.
Note that for even  , the power series proceed in even powers
of
, the power series proceed in even powers
of  . These eigenfunctions are said to have even parity: if
you replace
. These eigenfunctions are said to have even parity: if
you replace  by
by 
 , they are unchanged. Similarly, the
eigenfunctions for odd
, they are unchanged. Similarly, the
eigenfunctions for odd  expand in odd powers of
expand in odd powers of  . They
are said to have odd parity; if you replace
. They
are said to have odd parity; if you replace  by
by 
 , they
change sign.
, they
change sign.
![]() -
-![]()
![]()
![]()
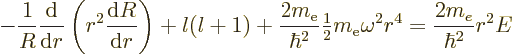

![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]() ,
,![]()
![]() .
.![]()
![]()
![]() ,
,