| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.28 Kirchhoff’s law
Suppose you have a material in thermodynamic equilibrium at a given
temperature that has an emissivity at a given frequency that exceeds
the corresponding absorptivity. Place it in a closed box. Since it
emits more radiation at the given frequency than it absorbs from the
surrounding blackbody radiation, the amount of radiation at that
frequency will go up. That violates Plank’s blackbody spectrum,
because it remains a closed box. The case that the emissivity is less
than the absorptivity goes similarly.
Note some of the implicit assumptions made in the argument. First, it
assumes linearity, in the sense that emission or absorption at one
frequency does not affect that at another, that absorption does not
affect emission, and that the absorptivity is independent of the
amount absorbed. It assumes that the surface is separable from the
object you are interested in. Transparent materials require special
consideration, but the argument that a layer of such material must
emit the same fraction of blackbody radiation as it absorbs remains
valid.
The argument also assumes the validity of Plank’s blackbody
spectrum. However you can make do without. Kirchhoff did. He (at
first) assumed that there are gage materials that absorb and emit only
in a narrow range of frequencies, and that have constant absorptivity
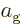 and emissivity
and emissivity 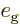 in that range. Place a plate
of that gage material just above a plate of whatever material is to be
examined. Insulate the plates from the surrounding. Wait for thermal
equilibrium.
in that range. Place a plate
of that gage material just above a plate of whatever material is to be
examined. Insulate the plates from the surrounding. Wait for thermal
equilibrium.
Outside the narrow frequency range, the material being examined will
have to absorb the same radiation energy that it emits, since the gage
material does not absorb nor emit outside the range. In the narrow
frequency range, the radiation energy 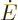 going up to the gage
plate must equal the energy coming down from it again, otherwise the
gage plate would continue to heat up. If
going up to the gage
plate must equal the energy coming down from it again, otherwise the
gage plate would continue to heat up. If  is the blackbody value
for the radiation in the narrow frequency range, then the energy going
down from the gage plate consists of the radiation that the gage plate
emits plus the fraction of the incoming radiation that it reflects
instead of absorbs:
is the blackbody value
for the radiation in the narrow frequency range, then the energy going
down from the gage plate consists of the radiation that the gage plate
emits plus the fraction of the incoming radiation that it reflects
instead of absorbs:
Similarly for the radiation going up from the material being examined:
By comparing the two results, 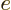



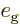

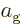 . Since you can examine any material
in this way, all materials must have the same ratio of emissivity to
absorptivity in the narrow range. Assuming that gage materials exist
for every frequency range, at any frequency
. Since you can examine any material
in this way, all materials must have the same ratio of emissivity to
absorptivity in the narrow range. Assuming that gage materials exist
for every frequency range, at any frequency 

 must be the same
for all materials. So it must be the blackbody value 1.
must be the same
for all materials. So it must be the blackbody value 1.
No, this book does not know where to order these gage materials,
[38]. And the same argument cannot be used to show
that the absorptivity must equal emissivity in each individual
direction of radiation, since direction is not preserved in
reflections.
![]()
![]()
![]()
![]()