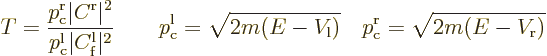| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.32 The evolution of probability
This note looks at conservation of probability, and the resulting
definitions of the reflection and transmission coefficients in
scattering. It also explains the concept of the “probability
current” that you may occasionally run into.
For the unsteady Schrödinger equation to provide a physically
correct description of nonrelativistic quantum mechanics, particles
should not be able to disappear into thin air. In particular, during
the evolution of the wave function of a single particle, the total
probability of finding the particle if you look everywhere should stay
one at all times:
Fortunately, the Schrödinger equation
does indeed conserve this total probability, so all is well.
To verify this, note first that 

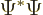 ,
where the star indicates the complex conjugate, so
,
where the star indicates the complex conjugate, so
To get an expression for that, take the Schrödinger equation above
times 

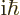 and add the complex conjugate of the
Schrödinger equation,
and add the complex conjugate of the
Schrödinger equation,
times 


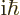 . The potential energy terms drop
out, and what is left is
. The potential energy terms drop
out, and what is left is
Now it can be verified by differentiating out that the right hand side
can be rewritten as a derivative:
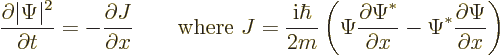 |
(A.232) |
For reasons that will become evident below, 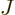 is called the
“probability current.” Note that
is called the
“probability current.” Note that 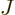 , like
, like  ,
will be zero at infinite
,
will be zero at infinite  for proper, normalized wave functions.
for proper, normalized wave functions.
If (A.232) is integrated over all  , the desired
result is obtained:
, the desired
result is obtained:
Therefore, the total probability of finding the particle does not
change with time. If a proper initial condition is provided to the
Schrödinger equation in which the total probability of finding the
particle is one, then it stays one for all time.
It gets a little more interesting to see what happens to the
probability of finding the particle in some given finite region 



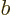 . That probability is given by
. That probability is given by
and it can change with time. A wave packet might enter or leave the
region. In particular, integration of (A.232) gives
This can be understood as follows: 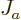 is the probability flowing
out of the region
is the probability flowing
out of the region 
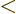
 into the interval
into the interval ![$[a,b]$](img5172.gif) through the
end
through the
end  . That increases the probability within
. That increases the probability within ![$[a,b]$](img5172.gif) .
Similarly,
.
Similarly, 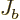 is the probability flowing out of
is the probability flowing out of ![$[a,b]$](img5172.gif) at
at 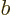 into
the region
into
the region 

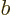 ; it decreases the probability within
; it decreases the probability within
![$[a,b]$](img5172.gif) . Now you see why
. Now you see why 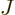 is called probability current; it
is equivalent to a stream of probability in the positive
is called probability current; it
is equivalent to a stream of probability in the positive
 -direction.
-direction.
The probability current can be generalized to more dimensions using
vector calculus:
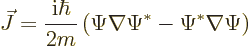 |
(A.233) |
and the net probability flowing out of a region is given by
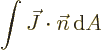 |
(A.234) |
where  is the outside surface area of the region, and
is the outside surface area of the region, and  is a
unit vector normal to the surface. A surface integral like this can
often be simplified using the divergence (Gauss or whatever) theorem
of calculus.
is a
unit vector normal to the surface. A surface integral like this can
often be simplified using the divergence (Gauss or whatever) theorem
of calculus.
Returning to the one-dimensional case, it is often desirable to relate
conservation of probability to the energy eigenfunctions of the
Hamiltonian,
because the energy eigenfunctions are generic, not specific to one
particular example wave function  .
.
To do so, first an important quantity called the “Wronskian” must be introduced. Consider any two eigenfunctions
 and
and  of the Hamiltonian:
of the Hamiltonian:
If you multiply the first equation above by  , the second
by
, the second
by  and then subtract the two, you get
and then subtract the two, you get
The constant 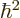

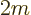 can be divided out, and by differentiation
it can be verified that the remainder can be written as
can be divided out, and by differentiation
it can be verified that the remainder can be written as
The quantity 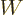 is called the Wronskian. It is the same at all
values of
is called the Wronskian. It is the same at all
values of  .
.
As an application, consider the example potential of figure
A.11 in addendum {A.27} that bounces a
particle coming in from the far left back to where it came from. In
the left region, the potential  has a constant value
has a constant value
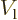 . In this region, an energy eigenfunction is of the
form
. In this region, an energy eigenfunction is of the
form
At the far right, the potential grows without bound and the
eigenfunction becomes zero rapidly. To make use of the Wronskian,
take the first solution  to be
to be 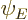 itself, and
itself, and  to be its complex conjugate
to be its complex conjugate 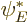 . Since at the far right
the eigenfunction becomes zero rapidly, the Wronskian is zero there.
And since the Wronskian is constant, that means it must be zero
everywhere. Next, if you plug the above expression for the
eigenfunction in the left region into the definition of the Wronskian
and clean up, you get
. Since at the far right
the eigenfunction becomes zero rapidly, the Wronskian is zero there.
And since the Wronskian is constant, that means it must be zero
everywhere. Next, if you plug the above expression for the
eigenfunction in the left region into the definition of the Wronskian
and clean up, you get
If that is zero, the magnitude of 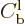 must be the
same as that of
must be the
same as that of 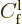 .
.
This can be understood as follows: if a wave packet is created from
eigenfunctions with approximately the same energy, then the terms
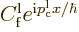 combine for
large negative times into a wave packet coming in from the far left.
The probability of finding the particle in that wave packet is
proportional to the integrated square magnitude of the wave function,
hence proportional to the square magnitude of
combine for
large negative times into a wave packet coming in from the far left.
The probability of finding the particle in that wave packet is
proportional to the integrated square magnitude of the wave function,
hence proportional to the square magnitude of
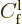 . For large positive times, the
. For large positive times, the
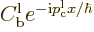 terms
combine in a similar wave packet, but one that returns towards the far
left. The probability of finding the particle in that departing wave
packet must still be the same as that for the incoming packet, so the
square magnitude of
terms
combine in a similar wave packet, but one that returns towards the far
left. The probability of finding the particle in that departing wave
packet must still be the same as that for the incoming packet, so the
square magnitude of 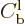 must be the same as that of
must be the same as that of
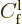 .
.
Next consider a generic scattering potential like the one in figure
7.22. To the far left, the eigenfunction is again of the
form
while at the far right it is now of the form
The Wronskian can be found the same way as before:
The fraction of the incoming wave packet that ends up being reflected
back towards the far left is called the “reflection coefficient”  . Following the same
reasoning as above, it can be computed from the coefficients in the
far left region of constant potential as:
. Following the same
reasoning as above, it can be computed from the coefficients in the
far left region of constant potential as:
The reflection coefficient gives the probability that the particle can
be found to the left of the scattering region at large times.
Similarly, the fraction of the incoming wave packet that passes
through the potential barrier towards the far right is called the
“transmission coefficient” 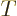 . It gives the probability
that the particle can be found to the right of the scattering region
at large times. Because of conservation of probability,
. It gives the probability
that the particle can be found to the right of the scattering region
at large times. Because of conservation of probability, 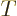

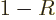 .
.
Alternatively, because of the Wronskian expression above, the
transmission coefficient can be explicitly computed from the
coefficient of the eigenfunction in the far right region as
If the potential energy is the same at the far right and far left, the
two classical momenta are the same, 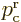

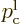 . Otherwise, the reason that the ratio of
classical momenta appears in the transmission coefficient is because
the classical momenta in a wave packet have a different spacing with
respect to energy if the potential energy is different. (The above
expression for the transmission coefficient can also be derived
explicitly using the Parseval equality of Fourier analysis, instead of
inferred from conservation of probability and the constant Wronskian.)
. Otherwise, the reason that the ratio of
classical momenta appears in the transmission coefficient is because
the classical momenta in a wave packet have a different spacing with
respect to energy if the potential energy is different. (The above
expression for the transmission coefficient can also be derived
explicitly using the Parseval equality of Fourier analysis, instead of
inferred from conservation of probability and the constant Wronskian.)
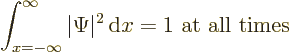
![]()
![]()
![]() ,
,
![]() ,
,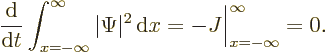
![]()
![]()
![]()
![]()
![]() .
.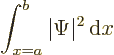
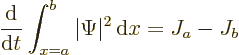
![]()
![]()
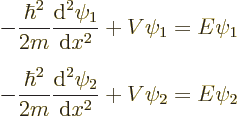

![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]() .
.![]() .
.
![]() .
.![]()
![]()
![]() .
.