| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
N.23 Fundamental assumption of statistics
The assumption that all energy eigenstates with the same energy are
equally likely is simply stated as an axiom in typical books,
[4, p. 92], [18, p. 1],
[25, p. 230], [52, p. 177]. Some of these
sources quite explicitly suggest that the fact should be self-evident
to the reader.
However, why could not an energy eigenstate, call it A, in which all
particles have about the same energy, have a wildly different
probability from some eigenstate B in which one particle has almost
all the energy and the rest has very little? The two wave functions
are wildly different. (Note that if the probabilities are only
somewhat different, it would not affect various conclusions much
because of the vast numerical superiority of the most probable energy
distribution.)
The fact that it does not take any energy to go from one state to the
other [18, p. 1] does not imply that the system must spend
equal time in each state, or that each state must be equally likely.
It is not difficult at all to construct nonlinear systems of evolution
equations that conserve energy and in which the system runs
exponentially away towards specific states.
However, the coefficients of the energy eigenfunctions do not satisfy
some arbitrary nonlinear system of evolution equations. They evolve
according to the Schrödinger equation, and the interactions between
the energy eigenstates are determined by a Hamiltonian matrix of
coefficients. The Hamiltonian is a Hermitian matrix; it has to be to
conserve energy. That means that the coupling constant that allows
state A to increase or reduce the probability of state B is just as
big as the coupling constant that allows B to increase or reduce the
probability of state A. More specifically, the rate of increase of
the probability of state A due to state B and vice-versa is seen to be

where 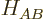 is the perturbation Hamiltonian coefficient between A
and B. (In the absence of perturbations, the energy eigenfunctions do
not interact and
is the perturbation Hamiltonian coefficient between A
and B. (In the absence of perturbations, the energy eigenfunctions do
not interact and 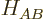
 0.) Assuming that the phase of the
Hamiltonian coefficient is random compared to the phase difference
between A and B, the transferred probability can go at random one way
or the other regardless of which one state is initially more likely.
Even if A is currently very improbable, it is just as likely to pick
up probability from B as B is from A. Also note that eigenfunctions of
the same energy are unusually effective in exchanging probability,
since their coefficients evolve approximately in phase.
0.) Assuming that the phase of the
Hamiltonian coefficient is random compared to the phase difference
between A and B, the transferred probability can go at random one way
or the other regardless of which one state is initially more likely.
Even if A is currently very improbable, it is just as likely to pick
up probability from B as B is from A. Also note that eigenfunctions of
the same energy are unusually effective in exchanging probability,
since their coefficients evolve approximately in phase.
This note would argue that under such circumstances, it is simply no
longer reasonable to think that the difference in probabilities
between eigenstates of the same energy is enough to make a difference.
How could energy eigenstates that readily and randomly exchange
probability, in either direction, end up in a situation where some
eigenstates have absolutely nothing, to incredible precision?
Feynman [18, p. 8] gives an argument based on
time-dependent perturbation theory, chapter 11.10. However,
time-dependent perturbations theory relies heavily on approximation,
and worse, the measurement wild card. Until scientists, while maybe
not agreeing exactly on what measurement is, start laying down
rigorous, unambiguous, mathematical ground rules on what measurements
can do and cannot do, measurement is like astrology: anything goes.
