| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
14.7 Draft: Binding energy
The binding energy of a nucleus is the energy that would be needed to
take it apart into its individual protons and neutrons. Binding
energy explains the overall trends in nuclear reactions.
Figure 14.4:
Binding energy per nucleon.
[pdf][con]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,56...
...makebox(0,0)[l]{$\fourIdx{62}{28}{}{}{\rm Ni}$}}
}
\end{picture}
\end{figure}](img3078.gif) |
As explained in the previous section, the binding energy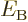 
can be found from the mass of the nucleus. The specific binding
energy is defined as the binding energy per nucleon,
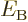
. Figure 14.4 shows the specific
binding energy of the nuclei with known masses. The highest specific
binding energy is 8.8 MeV, and occurs for
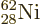nickel. Nickel has 28 protons, a
magic number. However, nonmagic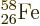 
and
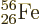are right on its heels.
Nuclei can therefore lower their total energy by evolving towards the
nickel-iron region. Light nuclei can “fusion” together into heavier ones to do so. Heavy nuclei can
emit alpha particles or fission, fall apart in smaller pieces.
Figure 14.4 also shows that the binding energy of most
nuclei is roughly 8 MeV per nucleon. However, the very light nuclei
are an exception; they tend to have a quite small binding energy per
nucleon. In a light nucleus, each nucleon only experiences attraction
from a small number of other nucleons. For example, deuterium only
has a binding energy of 1.1 MeV per nucleon.
The big exception to the exception is the doubly magic
nucleus, the alpha particle. It has a
stunning 7.07 MeV binding energy per nucleon, exceeding its immediate
neighbors by far.
The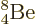 
beryllium nucleus is not bad either,
also with 7.07 MeV per nucleon, almost exactly as high as
, though admittedly that is
achieved using eight nucleons instead of only four. But clearly,
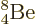is a lot more tightly bound than its
immediate neighbors.
It is therefore ironic that while various of those neighbors are
stable, the much more tightly bound 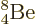is
not. It falls apart in about 67 as (i.e. 67 10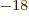
s), a tragic
consequence of being able to come neatly apart into two alpha
particles that are just a tiny bit more tightly bound. It is the only
alpha decay among the light nuclei. It is an exception to the rule
that light nuclei prefer to fusion into heavier ones.
But despite its immeasurably short half-life, do not think that
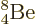is not important. Without it there
would be no life on earth. Because of the absence of stable
intermediaries, the Big Bang produced no elements heavier than
beryllium, (and only trace amounts of that) including no carbon. As
Hoyle pointed out, the carbon of life is formed in the interior of
aging stars when 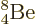captures a third alpha
particle, to produce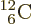 
, which is
stable. This is called the “triple alpha process.” Under the extreme conditions in the
interior of collapsing stars, given time this process produces
significant amounts of carbon despite the extremely short half-life of
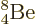. The process is far too slow to
have occurred in the Big Bang, however.
For 
carbon, the superior number of
nucleons has become big enough to overcome the doubly magic advantage
of the three corresponding alpha particles. Carbon-12’s binding
energy is 7.68 MeV per nucleon, greater than that of alpha particles.
