| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.1 Generic vector identities
The rules of engagement are as follows:
- The Cartesian axes are numbered using an index
 , with
, with

 1, 2, and 3 for
1, 2, and 3 for  ,
,  , and
, and  respectively.
respectively.
- Also,
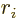 indicates the coordinate in the
indicates the coordinate in the  direction,
direction,
 ,
,  , or
, or  .
.
- Derivatives with respect to a coordinate
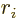 are indicated by
a simple subscript
are indicated by
a simple subscript  .
.
- If the quantity being differentiated is a vector, a comma is
used to separate the vector index from differentiation ones.
- Index
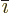 is the number immediately following
is the number immediately following  in the
cyclic sequence ...123123...and
in the
cyclic sequence ...123123...and 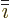 is the number
immediately preceding
is the number
immediately preceding  .
.
The first identity to be derived involves the “vectorial triple
product:”
 |
(D.1) |
To do so, first note that the  -th component of
-th component of 

 is given by
is given by
Repeating the rule, the  -th component of
-th component of 



 is
is
That writes out to
since the first and fourth terms cancel each other. The first three
terms can be recognized as the  -th component of
-th component of
 and the last three as the
and the last three as the  -th
component of
-th
component of  .
.
A second identity to be derived involves the “scalar triple
product:”
 |
(D.2) |
This is easiest derived from simply writing it out. The left hand
side is
while the right hand side is
Inspection shows it to be the same terms in a different order. Note
that since no order changes occur, the three vectors may be
noncommuting operators.