| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
5.3 Two-State Systems
Two-state systems are systems in which only two quantum states are of
importance. That makes such systems the simplest nontrivial quantum
systems. A lot of qualitative understanding can be obtained from
them. Among others, this section will shed some light on the reason
why chemical bonds tend to involve pairs of electrons.
As seen in chapter 4.6, the protons in the H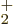 hydrogen
molecular ion are held together by a single shared electron. However,
in the H
hydrogen
molecular ion are held together by a single shared electron. However,
in the H neutral hydrogen molecule of the previous section, they
are held together by a shared pair of electrons. In both cases a
stable bond was formed. So why are chemical bonds involving a single
electron relatively rare, while bonds involving pairs of shared
electrons are common?
neutral hydrogen molecule of the previous section, they
are held together by a shared pair of electrons. In both cases a
stable bond was formed. So why are chemical bonds involving a single
electron relatively rare, while bonds involving pairs of shared
electrons are common?
The unifying concept relating the two bonds is that of two-state
systems. Such systems involve two intuitive basic states  and
and
 .
.
For the hydrogen molecular ion, one state, 

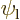 , described that the electron was in the ground
state around the left proton. A physically equivalent state,
, described that the electron was in the ground
state around the left proton. A physically equivalent state, 

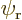 , had the electron in the ground state
around the right proton. For the hydrogen molecule,
, had the electron in the ground state
around the right proton. For the hydrogen molecule, 

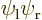 had electron 1 around the left proton and
electron 2 around the right one. The other state
had electron 1 around the left proton and
electron 2 around the right one. The other state 

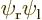 was physically the same, but it had the
electrons reversed.
was physically the same, but it had the
electrons reversed.
There are many other physical situations that may be described as two
state systems. Covalent chemical bonds involving atoms other than
hydrogen would be an obvious example. Just substitute a positive ion
for one or both protons.
As another example of a two-state system, consider the
C H
H “benzene molecular ring.” This molecule consists of a hexagon of
6 carbon atoms that are held together by 9 covalent bonds. The
logical way that 9 bonds can be arranged between the atoms of a 6 atom
ring is to make every second bond a double one. However, that still
leaves two possibilities; the locations of the single and double bonds
can be swapped. So there are once again two different but equivalent
states
“benzene molecular ring.” This molecule consists of a hexagon of
6 carbon atoms that are held together by 9 covalent bonds. The
logical way that 9 bonds can be arranged between the atoms of a 6 atom
ring is to make every second bond a double one. However, that still
leaves two possibilities; the locations of the single and double bonds
can be swapped. So there are once again two different but equivalent
states  and
and  .
.
The NH “ammonia molecule” consists of an nitrogen atom bonded to three
hydrogen atoms. By symmetry, the logical place for the nitrogen atom
to sit would surely be in the center of the triangle formed by the
three hydrogen atoms. But it does not sit there. If it was in the
center of the triangle, the angles between the hydrogen atoms,
measured from the nitrogen nucleus, should be 120
“ammonia molecule” consists of an nitrogen atom bonded to three
hydrogen atoms. By symmetry, the logical place for the nitrogen atom
to sit would surely be in the center of the triangle formed by the
three hydrogen atoms. But it does not sit there. If it was in the
center of the triangle, the angles between the hydrogen atoms,
measured from the nitrogen nucleus, should be 120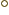 each.
However, as discussed later in chapter 5.11.3, valence bond
theory requires that the angles should be about 90
each.
However, as discussed later in chapter 5.11.3, valence bond
theory requires that the angles should be about 90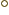 , not
120
, not
120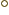 . (The actual angles are about 108
. (The actual angles are about 108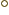 because of reasons similar to those for water as discussed in chapter
5.11.3.) The key point here is that the nitrogen must sit to
the side of the triangle, and there are two sides, producing once
again two different but equivalent physical states
because of reasons similar to those for water as discussed in chapter
5.11.3.) The key point here is that the nitrogen must sit to
the side of the triangle, and there are two sides, producing once
again two different but equivalent physical states  and
and
 .
.
In each case described above, there are two intuitive physical states
 and
and  . The peculiarities of the quantum
mechanics of two-state systems arise from states that are combinations
of these two states, as in
. The peculiarities of the quantum
mechanics of two-state systems arise from states that are combinations
of these two states, as in
Note that according to the ideas of quantum mechanics, the square
magnitude of the first coefficient of the combined state,
 , represents the probability of being in state
, represents the probability of being in state  and
and 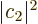 the probability of being in state
the probability of being in state  . Of
course, the total probability of being in one of the states should be
one:
. Of
course, the total probability of being in one of the states should be
one:
(This is only true if the  and
and  states are
orthonormal. In the hydrogen molecule cases, orthonormalizing the
basic states would change them a bit, but their physical nature would
remain much the same, especially if the protons are not too close.)
states are
orthonormal. In the hydrogen molecule cases, orthonormalizing the
basic states would change them a bit, but their physical nature would
remain much the same, especially if the protons are not too close.)
The key question is now what combination of states has the lowest
energy. That will be the ground state  of the
two-state system. The expectation value of energy is
of the
two-state system. The expectation value of energy is
This can be multiplied out, taking into account that numerical factors
come out of the left of an inner product as complex conjugates. The
result is
using the shorthand notation
Note that 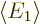 and
and 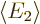 are real,
(2.16). They are the expectation energies of the states
are real,
(2.16). They are the expectation energies of the states
 and
and  . The states will be ordered so that
. The states will be ordered so that
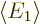 is less or equal to
is less or equal to 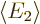 .
(In all the examples mentioned so far,
.
(In all the examples mentioned so far, 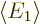 and
and
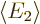 are equal because the two states are physically
equivalent.) Normally,
are equal because the two states are physically
equivalent.) Normally, 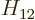 and
and 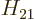 are not real but complex
conjugates, (2.16). However, you can always change the
definition of, say,
are not real but complex
conjugates, (2.16). However, you can always change the
definition of, say,  by a complex factor of magnitude one to
make
by a complex factor of magnitude one to
make 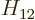 equal to a real and negative number, and then
equal to a real and negative number, and then 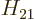 will be that same negative number.
will be that same negative number.
The above expression for the expectation energy consists of two kinds
of terms, which will be called:
Each of those contributions will be discussed in turn.
The averaged energy is the energy that you would intuitively expect
the combined wave function to have. It is a straightforward sum
of the expectation energies of the two component states  and
and
 times the probabilities of being in those states. In
particular, in the important case that the two states have the same
energy, the averaged energy is that energy. What is more logical than
that any mixture of two states with the same energy would have that
energy too?
times the probabilities of being in those states. In
particular, in the important case that the two states have the same
energy, the averaged energy is that energy. What is more logical than
that any mixture of two states with the same energy would have that
energy too?
But the twilight terms throw a monkey wrench in this simplistic
thinking. It can be seen that they will always make the ground state
energy 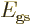 lower than the lowest energy of the component
states
lower than the lowest energy of the component
states 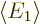 . (To see that, just take
. (To see that, just take 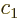 and
and
 positive real numbers and
positive real numbers and  small enough that
small enough that 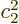 can be
neglected.) This lowering of the energy below the lowest component
state comes out of the mathematics of combining states; absolutely no
new physical forces are added to produce it. But if you try to
describe it in terms of classical physics, it really looks like a
mysterious new
can be
neglected.) This lowering of the energy below the lowest component
state comes out of the mathematics of combining states; absolutely no
new physical forces are added to produce it. But if you try to
describe it in terms of classical physics, it really looks like a
mysterious new twilight force
is in operation here.
It is no new force; it is the weird mathematics of quantum mechanics.
So, what are these twilight terms physically? If you mean,
what are they in terms of classical physics, there is simply no
answer. But if you mean, what are they in terms of normal language,
rather than formulae, it is easy. Just have another look at the
definition of the twilight terms; they are a measure of the inner
product 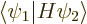 . That is the energy you
would get if nature was in state
. That is the energy you
would get if nature was in state  if nature was in state
if nature was in state
 . On quantum scales, nature can get really, really
ethereal, where it moves beyond being describable by classical
physics, and the result is very concrete, but weird, interactions.
For, at these scales twilight is real, and classical physics is not.
. On quantum scales, nature can get really, really
ethereal, where it moves beyond being describable by classical
physics, and the result is very concrete, but weird, interactions.
For, at these scales twilight is real, and classical physics is not.
For the twilight terms to be nonzero, there must be a region where the
two states overlap, i.e. there must be a region where both  and
and  are nonzero. In the simplest case of the hydrogen
molecular ion, if the atoms are far apart, the left and right wave
functions do not overlap and the twilight terms will be zero. For the
hydrogen molecule, it gets a bit less intuitive, since the overlap
should really be visualized in the six-dimensional space of those
functions. But still, the terms are zero when the atoms are far
apart.
are nonzero. In the simplest case of the hydrogen
molecular ion, if the atoms are far apart, the left and right wave
functions do not overlap and the twilight terms will be zero. For the
hydrogen molecule, it gets a bit less intuitive, since the overlap
should really be visualized in the six-dimensional space of those
functions. But still, the terms are zero when the atoms are far
apart.
The twilight terms are customarily referred to as “exchange terms,” but everybody seems to have a different idea
of what that is supposed to mean. The reason may be that these terms
pop up all over the place, in all sorts of very different settings.
This book prefers to call them twilight terms, since that most clearly
expresses what they really are. Nature is in a twilight zone of
ambiguity.
The lowering of the energy by the twilight terms produces more stable
chemical bonds than you would expect. Typically, the effect of the
terms is greatest if the two basic states  and
and  are
physically equivalent, like for the mentioned examples. Then the two
states have the same expectation energy, call it
are
physically equivalent, like for the mentioned examples. Then the two
states have the same expectation energy, call it
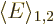 . For such symmetric systems, the
ground state will occur for an equal mixture of the two states,
. For such symmetric systems, the
ground state will occur for an equal mixture of the two states,
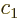



 , because then the
twilight terms are most negative. (Complex coefficients do not really
make a physical difference, so
, because then the
twilight terms are most negative. (Complex coefficients do not really
make a physical difference, so 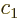 and
and  can be assumed to be
real numbers for convenience.) In the ground state, the lowest energy
is then an amount
can be assumed to be
real numbers for convenience.) In the ground state, the lowest energy
is then an amount 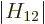 below the energy of the
component states:
below the energy of the
component states:
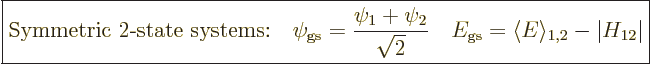 |
(5.13) |
On the other hand, if the lower energy state  has
significantly less energy than state
has
significantly less energy than state  , then the minimum
energy will occur near the lower energy state. That means that
, then the minimum
energy will occur near the lower energy state. That means that
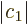
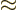 1 and
1 and 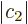
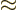 0. (This assumes that the
twilight terms are not big enough to dominate the energy.) In that
case
0. (This assumes that the
twilight terms are not big enough to dominate the energy.) In that
case 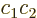
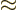 0 in the twilight terms (5.12), which
pretty much takes the terms out of the picture completely.
0 in the twilight terms (5.12), which
pretty much takes the terms out of the picture completely.
This happens for the single-electron bond of the hydrogen molecular
ion if the second proton is replaced by another ion, say a lithium
ion. The energy in state  , where the electron is around
the proton, will now be significantly less than that of state
, where the electron is around
the proton, will now be significantly less than that of state
 , where it is around the lithium ion. For such
asymmetrical single-electron bonds, the twilight terms are not likely
to help much in forging a strong bond. While it turns out that the
LiH
, where it is around the lithium ion. For such
asymmetrical single-electron bonds, the twilight terms are not likely
to help much in forging a strong bond. While it turns out that the
LiH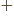 ion is stable, the binding energy is only 0.14 eV or so,
compared to 2.8 eV for the H
ion is stable, the binding energy is only 0.14 eV or so,
compared to 2.8 eV for the H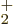 ion. Also, the LiH
ion. Also, the LiH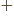 bond seems to be best described as a Van der Waals attraction, rather
than a true chemical bond.
bond seems to be best described as a Van der Waals attraction, rather
than a true chemical bond.
In contrast, for the two-electron bond of the neutral hydrogen
molecule, if the second proton is replaced by a lithium ion, states
 and
and  will still be the same: both states will have
one electron around the proton and one around the lithium ion. The
two states do have the electrons reversed, but the electrons are
identical. Thus the twilight terms are still likely to be effective.
Indeed neutral LiH lithium hydride exists as a stable molecule with a
binding energy of about 2.5 eV at low pressures.
will still be the same: both states will have
one electron around the proton and one around the lithium ion. The
two states do have the electrons reversed, but the electrons are
identical. Thus the twilight terms are still likely to be effective.
Indeed neutral LiH lithium hydride exists as a stable molecule with a
binding energy of about 2.5 eV at low pressures.
(It should be noted that the LiH bond is very ionic, with the
shared
electrons mostly at the hydrogen side, so the
actual ground state is quite different from the covalent hydrogen
model. But the model should be better when the nuclei are farther
apart, so the analysis can at least justify the existence of a
significant bond.)
For the ammonia molecule, the two states  and
and  differ
only in the side of the hydrogen triangle that the nitrogen atom is
at. Since these two states are physically equivalent, there is again
a significant lowering of the energy
differ
only in the side of the hydrogen triangle that the nitrogen atom is
at. Since these two states are physically equivalent, there is again
a significant lowering of the energy 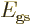 for the symmetric
combination
for the symmetric
combination 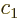

 . Similarly, there is a
significant raising of the energy
. Similarly, there is a
significant raising of the energy 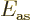 for the antisymmetric
combination
for the antisymmetric
combination 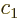

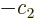 . Transitions between these two
energy states produce photons of a single energy in the microwave
range. It allows a maser (microwave-range laser) to be constructed.
The first maser was in fact an ammonia one. It gave rise to the
subsequent development of optical-range versions. These were
initially called
. Transitions between these two
energy states produce photons of a single energy in the microwave
range. It allows a maser (microwave-range laser) to be constructed.
The first maser was in fact an ammonia one. It gave rise to the
subsequent development of optical-range versions. These were
initially called optical masers,
but are now known as
lasers.
Masers are important for providing a single
frequency reference, like in some atomic clocks. See chapter
7.7 for the operating principle of masers and lasers.
The ammonia molecule may well be the best example of how weird these
twilight effects are. Consider, there are two common-sense states in
which the nitrogen is at one side of the hydrogen triangle. What
physical reason could there possibly be that there is a state of lower
energy in which the atom is at both sides at the same time with a
50/50 probability? Before you answer that, recall that it only works
if you do the 50/50 case right. If you do it wrong, you end up
raising the energy. And the only way to figure out whether you do it
right is to look at the behavior of the sign of a physically
unobservable wave function.
It may finally be noted that in the context of chemical bonds, the
raised-energy antisymmetric state is often called an “antibonding” state.
Key Points

- In quantum mechanics, the energy of different but physically
equivalent states can be lowered by mixing them together.

- This lowering of energy does not come from new physical forces,
but from the weird mathematics of the wave function.

- The effect tends to be much less when the original states are
physically very different.

- One important place where states are indeed physically the same
is in chemical bonds involving pairs of electrons. Here the
equivalent states merely have the identical electrons interchanged.
5.3 Review Questions
-
1.
-
The effectiveness of mixing states was already shown by the hydrogen molecule and molecular ion examples. But the generalized story above restricts the basis
states to be orthogonal, and the states used in the hydrogen examples were not.
Show that if  and
and  are not orthogonal states, but are normalized and produce a real and positive value for
are not orthogonal states, but are normalized and produce a real and positive value for 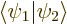 , like in the hydrogen examples, then orthogonal states can be found in the form
, like in the hydrogen examples, then orthogonal states can be found in the form
For normalized  and
and  the Cauchy-Schwartz inequality implies that
the Cauchy-Schwartz inequality implies that 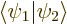 will be less than one. If the states do not overlap much, it will be much less than one and
will be less than one. If the states do not overlap much, it will be much less than one and  will be small.
will be small.
(If  and
and  do not meet the stated requirements, you can always redefine them by factors
do not meet the stated requirements, you can always redefine them by factors 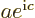 and
and 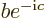 , with
, with  ,
, 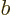 , and
, and  real, to get states that do.)
real, to get states that do.)
Solution 2state-a
-
2.
-
Show that it does not have an effect on the solution whether or not the basic states  and
and  are normalized, like in the previous question, before the state of lowest energy is found.
are normalized, like in the previous question, before the state of lowest energy is found.
This requires no detailed analysis; just check that the same solution can be described using the nonorthogonal and orthogonal basis states. It is however an important observation for various numerical solution procedures: your set of basis functions can be cleaned up and simplified without affecting the solution you get.
Solution 2state-b
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() H
H![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]() .
.![]()
![]() .
.![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()