| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
2.7 Additional Points
This subsection describes a few further issues of importance for this
book.
2.7.1 Dirac notation
Physicists like to write inner products such as 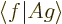 in
in Dirac notation
:
since this conforms more closely to how you would think of it
in linear algebra:
The various advanced ideas of linear algebra can be extended to
operators in this way, but they will not be needed in this book.
One thing will be needed in some more advanced addenda, however. That
is the case that operator  is not Hermitian. In that case,
if you want to take
is not Hermitian. In that case,
if you want to take  to the other side of the inner product, you
need to change it into a different operator. That operator is called
the “Hermitian conjugate” of
to the other side of the inner product, you
need to change it into a different operator. That operator is called
the “Hermitian conjugate” of  . In physics, it is almost
always indicated as
. In physics, it is almost
always indicated as 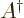 . So, simply by definition,
. So, simply by definition,
Then there are some more things that this book will not use. However,
you will almost surely encounter these when you read other books on
quantum mechanics.
First, the dagger is used much like a generalization of
complex conjugate,
etcetera. Applying a dagger a second time gives the original back.
Also, if you work out the dagger on a product, you need to reverse the
order of the factors. For example
In words, putting 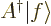 into the left side of an inner
product gives
into the left side of an inner
product gives 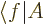 .
.
The second point will be illustrated for the case of vectors in
three dimensions. Such a vector can be written as
Here 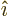 ,
, 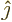 , and
, and  are the three unit
vectors in the axial directions. The components
are the three unit
vectors in the axial directions. The components 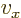 ,
,  and
and 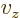 can be found using dot products:
can be found using dot products:
Symbolically, you can write this as
In fact, the operator in parentheses can be defined by saying
that for any vector  , it gives the exact same vector
back. Such an operator is called an “identity operator.”
, it gives the exact same vector
back. Such an operator is called an “identity operator.”
The relation
is called the “completeness relation.” To see why, suppose you leave off the
third part of the operator. Then
The  -component is gone! Now the vector
-component is gone! Now the vector  gets
projected onto the
gets
projected onto the 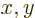 -plane. The operator has become a
“projection operator” instead of an identity operator by not
suming over the complete set of unit vectors.
-plane. The operator has become a
“projection operator” instead of an identity operator by not
suming over the complete set of unit vectors.
You will almost always find these things in terms of bras and kets.
To see how that looks, define
Then
so the completeness relation looks like
If you do not sum over the complete set of kets, you get a projection
operator instead of an identity one.
2.7.2 Additional independent variables
In many cases, the functions involved in an inner product may depend
on more than a single variable  . For example, they might
depend on the position
. For example, they might
depend on the position  in three-dimensional space.
in three-dimensional space.
The rule to deal with that is to ensure that the inner product
integrations are over all independent variables. For example,
in three spatial dimensions:
Note that the time  is a somewhat different variable from the rest,
and time is not included in the inner product integrations.
is a somewhat different variable from the rest,
and time is not included in the inner product integrations.
![]()

![]()
![]()
![]() .
.![]() .
.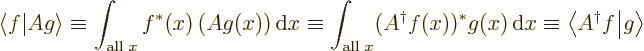
![]() .
.![]()
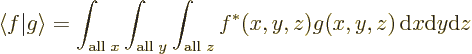
![]()