| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
12.8 Some important results
This section gives some results that are used frequently in quantum
analysis, but usually not explicitly stated.
First a note on notations. It is fairly common to use the letter  for orbital angular momentum,
for orbital angular momentum,  for spin, and
for spin, and  for combinations
of orbital and angular momentum. This subsection will follow these
conventions where appropriate.
for combinations
of orbital and angular momentum. This subsection will follow these
conventions where appropriate.
-
1.
- If all possible angular momentum states are filled
with a fermion, the resulting angular momentum is zero and the wave
function is spherically symmetric. For example, consider the
simplified case that there is one spinless fermion in each spherical
harmonic at a given azimuthal quantum number
 . Then it is
easy to see from the form of the spherical harmonics that the
combined wave function is independent of the angular position around
the
. Then it is
easy to see from the form of the spherical harmonics that the
combined wave function is independent of the angular position around
the  -axis. And all spherical harmonics at that
-axis. And all spherical harmonics at that  are filled
whatever you take to be the
are filled
whatever you take to be the  -axis. This makes noble gasses into
the equivalent of billiard balls. More generally, if there is one
fermion for every possible
-axis. This makes noble gasses into
the equivalent of billiard balls. More generally, if there is one
fermion for every possible direction
of the angular
momentum, by symmetry the net angular momentum can only be zero.
-
2.
- If a spin
 fermion has orbital angular
momentum quantum number
fermion has orbital angular
momentum quantum number  , net (orbital plus spin) angular
momentum quantum number
, net (orbital plus spin) angular
momentum quantum number 

 , and net
momentum in the
, and net
momentum in the  -direction quantum number
-direction quantum number 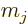 , its net
state is given in terms of the individual orbital and spin states
as:
, its net
state is given in terms of the individual orbital and spin states
as:
If the net spin is 

 , assuming that
, assuming that 
 0, that becomes
0, that becomes
Note that if the net angular momentum is unambiguous, the orbital
and spin magnetic quantum numbers  and
and  are in general
uncertain.
are in general
uncertain.
-
3.
- For identical particles, an important question is
how the Clebsch-Gordan coefficients change under particle exchange:
For 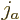

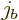

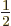 , this verifies that the
triplet states
, this verifies that the
triplet states 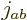
 1 are symmetric, and the singlet state
1 are symmetric, and the singlet state
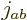
 0 is antisymmetric. More generally, states with the
maximum net angular momentum
0 is antisymmetric. More generally, states with the
maximum net angular momentum 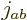

 and whole
multiples of 2 less are symmetric under particle exchange. States
that are odd amounts less than the maximum are antisymmetric under
particle exchange.
and whole
multiples of 2 less are symmetric under particle exchange. States
that are odd amounts less than the maximum are antisymmetric under
particle exchange.
-
4.
- When the net angular momentum state is swapped with
one of the component states, the relation is
This is of interest in figuring out what states produce zero net
angular momentum, 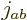

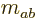
 0. In that case,
the right hand side is zero unless
0. In that case,
the right hand side is zero unless 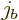

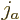 and
and 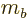

 ; and then
; and then 
 1. You can only create zero angular momentum from a pair of
particles that have the same square angular momentum; also, only
product states with zero net angular momentum in the
1. You can only create zero angular momentum from a pair of
particles that have the same square angular momentum; also, only
product states with zero net angular momentum in the  -direction
are involved.
-direction
are involved.
![]()
![]()
![]()


![\begin{eqnarray*}
\lefteqn{\langle j_{ab} m_{ab} \vert{\left\vert j_a\:m_a\righ...
...ngle} {\left\vert j_b\:\rule[2.5pt]{5pt}{.5pt}m_b\right\rangle}
\end{eqnarray*}](img2756.gif)