| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
12.9 Momentum of partially filled shells
One very important case of combining angular momenta occurs for both
electrons in atoms and nucleons in nuclei. In these problems there
are a number of identical fermions in single-particle states that
differ only in the net (orbital plus spin) momentum in the chosen
 -direction. Loosely speaking, the single-particle states are the
same, just at different angular orientations. Such a set of states is
often called a
-direction. Loosely speaking, the single-particle states are the
same, just at different angular orientations. Such a set of states is
often called a shell.
The question is then: what
combinations of the states are antisymmetric with respect to exchange
of the fermions, and therefore allowed? More specifically, what is
their combined net angular momentum?
Table 12.1:
Possible combined angular momentum of identical fermions in
shells of single-particle states that differ in magnetic quantum number.
The top shows odd numbers of particles, the bottom even numbers.
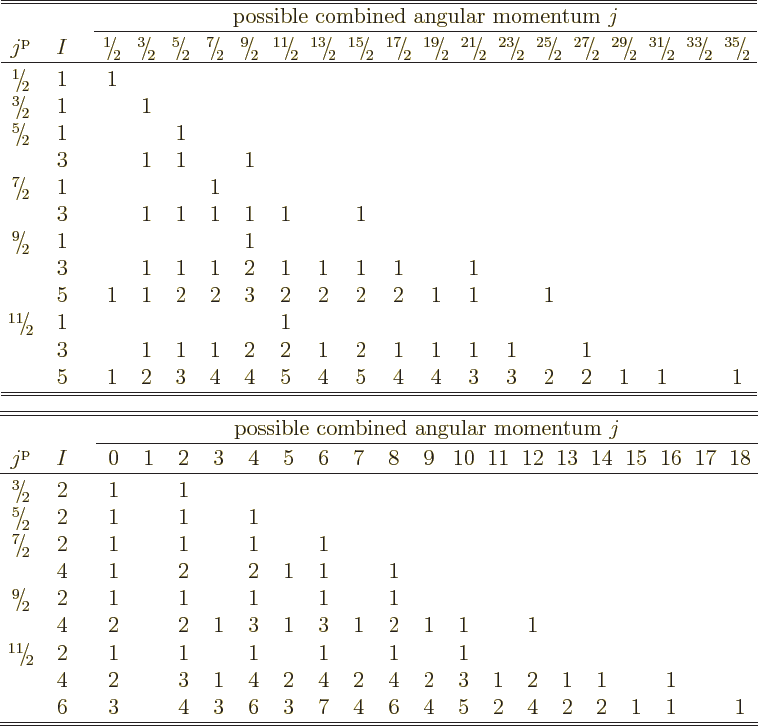 |
The answer is given in table 12.1, {D.67}.
In it,  is the number of fermions in the shell. Further
is the number of fermions in the shell. Further  is
the net angular momentum of the single-particle states that make up
the shell. (Or the azimuthal quantum number of that angular momentum
really.) Similarly the values of
is
the net angular momentum of the single-particle states that make up
the shell. (Or the azimuthal quantum number of that angular momentum
really.) Similarly the values of  indicate the possible net
angular momentum quantum numbers of all
indicate the possible net
angular momentum quantum numbers of all  fermions combined. The
main body of the table lists the multiplicity of sets with the given
angular momentum. Note that the table is split into odd and even
numbers of particles. That simplifies the presentation, because odd
numbers of particles produce only half-integer net angular momentum,
and even numbers only integer net angular momentum.
fermions combined. The
main body of the table lists the multiplicity of sets with the given
angular momentum. Note that the table is split into odd and even
numbers of particles. That simplifies the presentation, because odd
numbers of particles produce only half-integer net angular momentum,
and even numbers only integer net angular momentum.
For example, consider a single particle, 
 1, in a set of
single-particle states with angular momentum
1, in a set of
single-particle states with angular momentum 

 . For a single particle, the
. For a single particle, the combined
momentum  is simply the single particle momentum
is simply the single particle momentum  ,
explaining the single 1 in the
,
explaining the single 1 in the  column. But note that the 1
stands for a set of states; the magnetic net quantum number
column. But note that the 1
stands for a set of states; the magnetic net quantum number 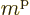 of
the single particle could still be any one of
of
the single particle could still be any one of  ,
,
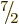 , ...,
, ...,  . All the ten states in
this set have net angular momentum
. All the ten states in
this set have net angular momentum 

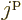

 .
.
Next assume that there are two particles in the same 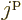

 single-particle states. Then if both particles would be in
the
single-particle states. Then if both particles would be in
the 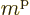

 single-particle state, their combined
angular momentum in the
single-particle state, their combined
angular momentum in the  -direction
-direction  would be 2
would be 2 

 9. Following the Clebsch-Gordan derivation shows
that this state would have combined angular momentum
9. Following the Clebsch-Gordan derivation shows
that this state would have combined angular momentum 


 9. But the two identical fermions cannot be both in the
9. But the two identical fermions cannot be both in the 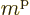

 state; that violates the Pauli exclusion principle.
That is why there is no entry in the
state; that violates the Pauli exclusion principle.
That is why there is no entry in the 
 9 column. If the first
particle is in the
9 column. If the first
particle is in the 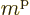

 state, the second one can
at most be in the
state, the second one can
at most be in the 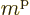

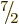 state, for a total of
state, for a total of 
 8. More precisely, the particles would have to be in the
antisymmetric combination, or Slater determinant, of these two
states. That antisymmetric combination can be seen to have combined
angular momentum
8. More precisely, the particles would have to be in the
antisymmetric combination, or Slater determinant, of these two
states. That antisymmetric combination can be seen to have combined
angular momentum 
 8. There are other combinations of states
that also have
8. There are other combinations of states
that also have 
 8, but values of
8, but values of  equal to 7, 6, ...,
equal to 7, 6, ...,
 8, for a total of 17 states. That set of 17 states is indicated by
the 1 in the
8, for a total of 17 states. That set of 17 states is indicated by
the 1 in the 
 8 column.
8 column.
It is also possible for the two 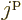

 particles to
combine their angular momentum into smaller even values of the total
angular momentum
particles to
combine their angular momentum into smaller even values of the total
angular momentum  . In fact, it is possible for the particles
to combine their angular momenta so that they exactly cancel one
another; then the net angular momentum
. In fact, it is possible for the particles
to combine their angular momenta so that they exactly cancel one
another; then the net angular momentum 
 0. That is indicated
by the 1 in the
0. That is indicated
by the 1 in the 
 0 column. Classically you would say that
the momentum vectors of the two particles are exactly opposite,
producing a zero resultant. In quantum mechanics true angular
momentum vectors do not exist due to uncertainty of the components,
but complete cancelation is still possible.
0 column. Classically you would say that
the momentum vectors of the two particles are exactly opposite,
producing a zero resultant. In quantum mechanics true angular
momentum vectors do not exist due to uncertainty of the components,
but complete cancelation is still possible.
The 
 0 set consists of just one state, because
0 set consists of just one state, because  can only be zero
for a state with zero angular momentum. The entire table row for two
can only be zero
for a state with zero angular momentum. The entire table row for two
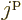

 particles could in principle be derived by writing
out the appropriate Clebsch-Gordan coefficients. But that would be
one very big table.
particles could in principle be derived by writing
out the appropriate Clebsch-Gordan coefficients. But that would be
one very big table.
If there are five 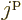

 particles. they can combine
their angular momenta into quite a wide variety of net angular
momentum values. For example, the 2 in the
particles. they can combine
their angular momenta into quite a wide variety of net angular
momentum values. For example, the 2 in the 

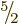 column indicates that there are two sets of states with combined
angular momentum
column indicates that there are two sets of states with combined
angular momentum 

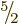 . Each set has 6 members,
because for each set
. Each set has 6 members,
because for each set  can be any one of
can be any one of 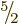 ,
,
 , ...,
, ..., 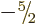 . So there are a total of
12 independent combination states that have net angular momentum
. So there are a total of
12 independent combination states that have net angular momentum 

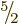 .
.
Note that a shell has 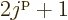 different single-particle states,
because the magnetic quantum number
different single-particle states,
because the magnetic quantum number 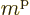 can have the values
can have the values
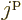 ,
, 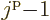 , ...,
, ..., 
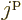 . Therefore a
shell can accommodate up to
. Therefore a
shell can accommodate up to 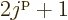 fermions according to the
exclusion principle. However, the table only lists combined angular
momentum values for up to
fermions according to the
exclusion principle. However, the table only lists combined angular
momentum values for up to  particles. The reason is
that any more is unnecessary. A given number of
particles. The reason is
that any more is unnecessary. A given number of holes
in an otherwise filled shell produces the same combined angular
momentum values as the same number of particles in an otherwise empty
shell. For example, two fermions in a 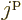

 shell,
(zero holes), have the same combined angular momentum as zero
particles: zero. Indeed, those two fermions must be in the
antisymmetric singlet state with spin zero. In general, a completely
filled shell has zero angular momentum and is spherically symmetric.
shell,
(zero holes), have the same combined angular momentum as zero
particles: zero. Indeed, those two fermions must be in the
antisymmetric singlet state with spin zero. In general, a completely
filled shell has zero angular momentum and is spherically symmetric.
Table 12.2:
Possible combined angular momentum of identical bosons.
 |
The same situation for identical bosons is shown in table
12.2. For identical bosons there is no limit to the
number of particles that can go into a shell. The table was
arbitrarily cut off at 9 particles and a maximum spin of 18.
![]() -
-
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 8
8![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]()