6.6 Bose-Ein­stein Con­den­sa­tion

This sec­tion ex­am­ines what hap­pens to a sys­tem of non­in­ter­act­ing bosons in a box if the tem­per­a­ture is some­what greater than ab­solute zero.

Fig­ure 6.3: The sys­tem of bosons at a very low tem­per­a­ture.

Fig­ure 6.4: The sys­tem of bosons at a rel­a­tively low tem­per­a­ture.

As noted in the sec­ond last sec­tion, in the ground state all bosons are in the sin­gle-par­ti­cle state of low­est en­ergy. This was in­di­cated by the fat blue dot next to the ori­gin in the wave num­ber space fig­ure 6.2. Nonzero tem­per­a­ture im­plies that the bosons ob­tain an ad­di­tional amount of en­ergy above the ground state. There­fore they will spread out a bit to­wards states of higher en­ergy. The sin­gle fat blue point will be­come a col­ored cloud as shown in fig­ures 6.3 and 6.4. So far, that all seems plau­si­ble enough.

But some­thing weird oc­curs for iden­ti­cal bosons:

Be­low a cer­tain crit­i­cal tem­per­a­ture a fi­nite frac­tion of the bosons re­mains bunched to­gether in the sin­gle-par­ti­cle state of low­est en­ergy.

That is in­di­cated by the fat blue dot in fig­ure 6.3. The low­est en­ergy state, the one clos­est to the ori­gin, holds less bosons than at ab­solute zero, but be­low a cer­tain crit­i­cal tem­per­a­ture, it re­mains a fi­nite frac­tion of the to­tal.

That is weird be­cause the av­er­age ther­mal en­ergy avail­able to each bo­son dwarfs the dif­fer­ence in en­ergy be­tween the low­est en­ergy sin­gle-par­ti­cle state and its im­me­di­ate neigh­bors. If the en­ergy dif­fer­ence be­tween the low­est en­ergy state and its neigh­bors is neg­li­gi­bly small, you would rea­son­ably ex­pect that they will hold sim­i­lar num­bers of bosons. And if a lot of states near the ori­gin each hold about the same num­ber of bosons, then that num­ber must be a small frac­tion of the to­tal, not a fi­nite one. But rea­son­able or not, it is un­true. For a sys­tem of non­in­ter­act­ing bosons be­low the crit­i­cal tem­per­a­ture, the low­est en­ergy state holds a fi­nite frac­tion of the bosons, much more than its im­me­di­ate neigh­bors.

If you raise the tem­per­a­ture of the sys­tem, you boil away the bosons in the low­est en­ergy state into the sur­round­ing cloud. Above the crit­i­cal tem­per­a­ture, the ex­cess bosons are gone and the low­est en­ergy state now only holds a sim­i­lar num­ber of bosons as its im­me­di­ate neigh­bors. That is il­lus­trated in fig­ure 6.4. Con­versely, if you lower the tem­per­a­ture of the sys­tem from above to be­low the crit­i­cal tem­per­a­ture, the bosons start con­dens­ing into the low­est en­ergy state. This process is called Bose-Ein­stein con­den­sa­tion af­ter Bose and Ein­stein who first pre­dicted it.

Bose-Ein­stein con­den­sa­tion is a pure quan­tum ef­fect; it is due to the sym­metriza­tion re­quire­ment for the wave func­tion. It does not oc­cur for fermi­ons, or if each par­ti­cle in the box is dis­tin­guish­able from every other par­ti­cle. Dis­tin­guish­able should here be taken to mean that there are no an­ti­sym­metriza­tion re­quire­ments, as there are not if each par­ti­cle in the sys­tem is a dif­fer­ent type of par­ti­cle from every other par­ti­cle.

It should be noted that the given de­scrip­tion is sim­plis­tic. In par­tic­u­lar, it is cer­tainly pos­si­ble to cool a mi­cro­scopic sys­tem of dis­tin­guish­able par­ti­cles down un­til say about half the par­ti­cles are in the sin­gle-par­ti­cle state of low­est en­ergy. Based on the above dis­cus­sion, you would then con­clude that Bose-Ein­stein con­den­sa­tion has oc­curred. That is not true. The prob­lem is that this sup­posed con­den­sa­tion dis­ap­pears when you scale up the sys­tem to macro­scopic di­men­sions and a cor­re­spond­ing macro­scopic num­ber of par­ti­cles.

Given a mi­cro­scopic sys­tem of dis­tin­guish­able par­ti­cles with half in the sin­gle-par­ti­cle ground state, if you hold the tem­per­a­ture con­stant while in­creas­ing the sys­tem size, the size of the cloud of oc­cu­pied states in wave num­ber space re­mains about the same. How­ever, the big­ger macro­scopic sys­tem has much more en­ergy states, spaced much closer to­gether in wave num­ber space. Dis­tin­guish­able par­ti­cles spread out over these ad­di­tional states, leav­ing only a van­ish­ingly small frac­tion in the low­est en­ergy state. This does not hap­pen if you scale up a Bose-Ein­stein con­den­sate; here the frac­tion of bosons in the low­est en­ergy state stays fi­nite re­gard­less of sys­tem size.

Bose-Ein­stein con­den­sa­tion was achieved in 1995 by Cor­nell, Wie­man, et al by cool­ing a di­lute gas of ru­bid­ium atoms to be­low about 170 nK (nano Kelvin). Based on the ex­tremely low tem­per­a­ture and fragility of the con­den­sate, prac­ti­cal ap­pli­ca­tions are very likely to be well into the fu­ture, and even de­ter­mi­na­tion of the con­den­sate’s ba­sic prop­er­ties will be dif­fi­cult.

A process sim­i­lar to Bose-Ein­stein con­den­sa­tion is also be­lieved to oc­cur in liq­uid he­lium when it turns into a su­per­fluid be­low 2.17 K. How­ever, this case is more tricky, {N.21}. For one, the atoms in liq­uid he­lium can hardly be con­sid­ered to be non­in­ter­act­ing. That makes the en­tire con­cept of sin­gle-par­ti­cle states poorly de­fined. Still, it is quite widely be­lieved that for he­lium be­low 2.17 K, a fi­nite frac­tion of the atoms starts ac­cu­mu­lat­ing in what is taken to be a sin­gle-par­ti­cle state of zero wave num­ber. Un­like for nor­mal Bose-Ein­stein con­den­sa­tion, for he­lium it is be­lieved that the num­ber of atoms in this state re­mains lim­ited. At ab­solute zero only about 9% of the atoms end up in the state.

Cur­rently there is a lot of in­ter­est in other sys­tems of par­ti­cles un­der­go­ing Bose-Ein­stein con­den­sa­tion. One ex­am­ple is liq­uid he­lium-3. Com­pared to nor­mal he­lium, he­lium-3 misses a neu­tron in its nu­cleus. That makes its spin half-in­te­ger, so it is not a bo­son but a fermion. There­fore, it should not turn into a su­per­fluid like nor­mal liq­uid he­lium. And it does not. He­lium 3 be­haves in al­most all as­pects ex­actly the same as nor­mal he­lium. It be­comes liq­uid at a sim­i­lar tem­per­a­ture, 3.2 K in­stead of 4.2 K. But it does not be­come a su­per­fluid like nor­mal he­lium at any tem­per­a­ture com­pa­ra­ble to 2.17 K. That is very strong ev­i­dence that the su­per­fluid be­hav­ior of nor­mal he­lium is due to the fact that it is a bo­son.

Still it turns out that at tem­per­a­tures three or­ders of mag­ni­tude smaller, he­lium-3 does turn into a su­per­fluid. That is be­lieved to be due to the fact that the atoms pair up. A com­pos­ite of two fermi­ons has in­te­ger spin, so it is a bo­son. Sim­i­larly, su­per­con­duc­tiv­ity of sim­ple solids is due to the fact that the elec­trons pair up into Cooper pairs. They get tied to­gether due to their in­ter­ac­tion with the sur­round­ing atoms.

A va­ri­ety of other par­ti­cles can pair up to. At the time of writ­ing, there is in­ter­est in po­lari­ton con­den­sates. A po­lari­ton is a quan­tum me­chan­i­cal su­per­po­si­tion of a pho­ton and an elec­tronic ex­ci­ta­tion in a solid. It is hoped that these will al­low Bose-Ein­stein con­den­sa­tion to be stud­ied at room tem­per­a­ture. There is still much to be learned about it. For ex­am­ple, while the re­la­tion­ship be­tween su­per­flu­id­ity and Bose-Ein­stein con­den­sa­tion is quite gen­er­ally ac­cepted, there are some is­sues. Snoke & Baym point out, (in the in­tro­duc­tion to Bose-Ein­stein Con­den­sa­tion, Grif­fin, A., Snoke, D.W., & Stringari, S., Eds, 1995, Cam­bridge), that ex­am­ples in­di­cate that Bose-Ein­stein con­den­sa­tion is nei­ther nec­es­sary nor suf­fi­cient for su­per­flu­id­ity. With only ap­prox­i­mate the­o­ret­i­cal mod­els and ap­prox­i­mate ex­per­i­men­tal data, it is of­ten dif­fi­cult to make solid spe­cific state­ments.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

In Bose-Ein­stein con­den­sa­tion, a fi­nite frac­tion of the bosons is in the sin­gle-par­ti­cle state of low­est en­ergy.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

It hap­pens when the tem­per­a­ture falls be­low a crit­i­cal value.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

It ap­plies to macro­scopic sys­tems.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The ef­fect is unique to bosons.

6.6.1 Rough ex­pla­na­tion of the con­den­sa­tion

The rea­son why bosons show Bose-Ein­stein con­den­sa­tion while sys­tems of dis­tin­guish­able par­ti­cles do not is com­plex. It is dis­cussed in chap­ter 11. How­ever, the idea can be ex­plained qual­i­ta­tively by ex­am­in­ing a very sim­ple sys­tem

Fig­ure 6.5: Ground state sys­tem en­ergy eigen­func­tion for a sim­ple model sys­tem. The sys­tem has only 6 sin­gle-par­ti­cle states; each of these has one of 3 en­ergy lev­els. In the spe­cific case shown here, the sys­tem con­tains 3 dis­tin­guish­able spin­less par­ti­cles. All three are in the sin­gle-par­ti­cle ground state. Left: math­e­mat­i­cal form. Right: graph­i­cal rep­re­sen­ta­tion.

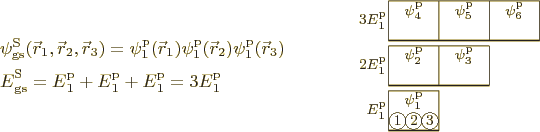As­sume that there are just three dif­fer­ent sin­gle-par­ti­cle en­ergy lev­els, with val­ues ${\vphantom' E}^{\rm p}_1$, $2{\vphantom' E}^{\rm p}_1$, and $3{\vphantom' E}^{\rm p}_1$. Also as­sume that there is just one sin­gle-par­ti­cle state with en­ergy ${\vphantom' E}^{\rm p}_1$, but two with en­ergy $2{\vphantom' E}^{\rm p}_1$ and 3 with en­ergy $3{\vphantom' E}^{\rm p}_1$. That makes a to­tal of 6 sin­gle par­ti­cle-states; they are shown as boxes that can hold par­ti­cles at the right hand side of fig­ure 6.5. As­sume also that there are just three par­ti­cles and for now take them to be dis­tin­guish­able. Fig­ure 6.5 then shows the sys­tem ground state in which every par­ti­cle is in the sin­gle-par­ti­cle ground state with en­ergy ${\vphantom' E}^{\rm p}_1$. That makes the to­tal sys­tem en­ergy $3{\vphantom' E}^{\rm p}_1$.

Fig­ure 6.6: Ex­am­ple sys­tem en­ergy eigen­func­tion with five times the sin­gle-par­ti­cle ground state en­ergy.

How­ever, now as­sume that the sys­tem is at a nonzero tem­per­a­ture. In par­tic­u­lar, as­sume that the to­tal sys­tem en­ergy is $5{\vphantom' E}^{\rm p}_1$. An ex­am­ple sys­tem en­ergy eigen­func­tion with that en­ergy is il­lus­trated in fig­ure 6.6.

Fig­ure 6.7: For dis­tin­guish­able par­ti­cles, there are 9 sys­tem en­ergy eigen­func­tions that have en­ergy dis­tri­b­u­tion A.

Fig­ure 6.8: For dis­tin­guish­able par­ti­cles, there are 12 sys­tem en­ergy eigen­func­tions that have en­ergy dis­tri­b­u­tion B.

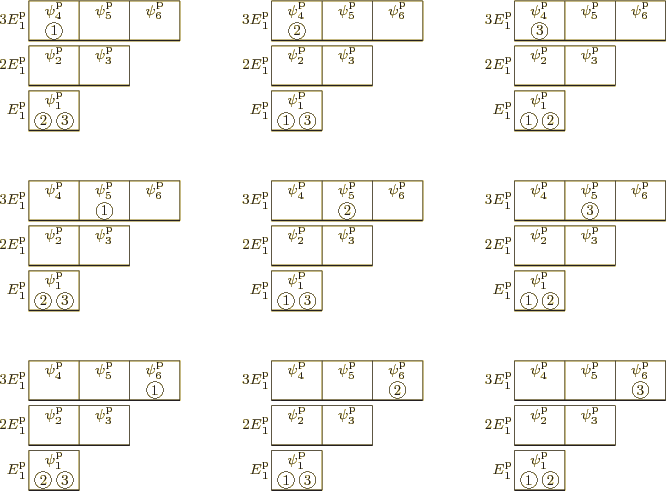
But there are a lot more sys­tem eigen­func­tions with en­ergy $5{\vphantom' E}^{\rm p}_1$. There are two gen­eral ways to achieve that en­ergy:

En­ergy dis­tri­b­u­tion A:

Two par­ti­cles in the ground state with en­ergy ${\vphantom' E}^{\rm p}_1$ and one in a state with en­ergy $3{\vphantom' E}^{\rm p}_1$.

En­ergy dis­tri­b­u­tion B:

One par­ti­cle in the ground state with en­ergy ${\vphantom' E}^{\rm p}_1$ and two in states with en­ergy $2{\vphantom' E}^{\rm p}_1$.

As fig­ures 6.7 and 6.8 show, there are 9 sys­tem en­ergy eigen­func­tions that have en­ergy dis­tri­b­u­tion A, but 12 that have en­ergy dis­tri­b­u­tion B.

There­fore, all else be­ing the same, en­ergy dis­tri­b­u­tion B is more likely to be ob­served than A!

Of course, the dif­fer­ence be­tween 9 sys­tem eigen­func­tions and 12 is mi­nor. Also, every­thing else is not the same; the eigen­func­tions dif­fer. But it turns out that if the sys­tem size is in­creased to macro­scopic di­men­sions, the dif­fer­ences in num­bers of en­ergy eigen­func­tions be­come gi­gan­tic. There will be one en­ergy dis­tri­b­u­tion for which there are as­tro­nom­i­cally more sys­tem eigen­func­tions than for any other en­ergy dis­tri­b­u­tion. Com­mon-sense sta­tis­tics then says that this en­ergy dis­tri­b­u­tion is the only one that will ever be ob­served. If there are count­less or­ders of mag­ni­tude more eigen­func­tions for a dis­tri­b­u­tion B than for a dis­tri­b­u­tion A, what are the chances of A ever be­ing found?

It is cu­ri­ous to think of it: only one en­ergy dis­tri­b­u­tion is ob­served for a given macro­scopic sys­tem. And that is not be­cause of any physics; other en­ergy dis­tri­b­u­tions are phys­i­cally just as good. It is be­cause of a math­e­mat­i­cal count; there are just so many more en­ergy eigen­func­tions with that dis­tri­b­u­tion.

Fig­ure 6.9: For iden­ti­cal bosons, there are only 3 sys­tem en­ergy eigen­func­tions that have en­ergy dis­tri­b­u­tion A.

Fig­ure 6.10: For iden­ti­cal bosons, there are also only 3 sys­tem en­ergy eigen­func­tions that have en­ergy dis­tri­b­u­tion B.

Bose-Ein­stein con­den­sa­tion has to do with the fact that the count of eigen­func­tions is dif­fer­ent for iden­ti­cal bosons than for dis­tin­guish­able par­ti­cles. The de­tails were worked out in chap­ter 5.7. The sym­metriza­tion re­quire­ment for bosons im­plies that sys­tem eigen­func­tions that are the same ex­cept for ex­changes of par­ti­cles must be com­bined to­gether into one. In par­tic­u­lar for dis­tri­b­u­tion A, in each of the rows of fig­ure 6.7 the eigen­func­tions are the same ex­cept for such ex­changes. Sim­ply put, they merely dif­fer in what num­ber is stamped on each par­ti­cle. There­fore, for each row, the eigen­func­tions must be com­bined to­gether into a sin­gle eigen­func­tion. That leaves only the three sys­tem eigen­func­tions shown in fig­ure 6.9.

In the com­bi­na­tion eigen­func­tion, every par­ti­cle oc­cu­pies every sin­gle-​par­ti­cle state in­volved equally. There­fore, num­bers on the par­ti­cles would not add any non­triv­ial in­for­ma­tion and may as well be left away. Sure, you could put all three num­bers 1,2, and 3 in each of the par­ti­cles in fig­ure 6.9. But what good would that do?

Com­par­ing fig­ures 6.7 and 6.9, you can see why par­ti­cles sat­is­fy­ing sym­metriza­tion re­quire­ments are com­monly called in­dis­tin­guish­able. Clas­si­cal quan­tum me­chan­ics may imag­ine to stamp num­bers on the three iden­ti­cal bosons to keep them apart, but you sure do not see the dif­fer­ence be­tween them in the sys­tem en­ergy eigen­func­tions.

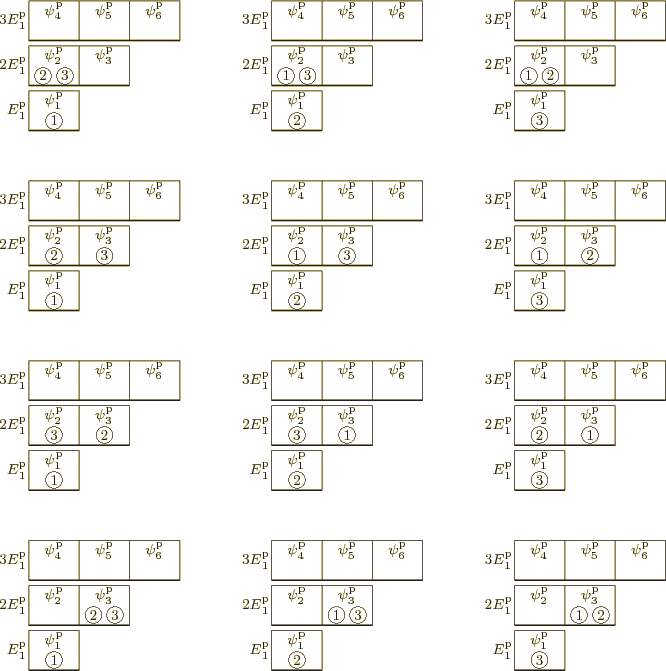
For dis­tri­b­u­tion B of fig­ure 6.8, un­der the sym­metriza­tion re­quire­ment the three en­ergy eigen­func­tions in the first row must be com­bined into one, the six in the sec­ond and third rows must be com­bined into one, and the three in the fourth row must be com­bined into one. That gives a to­tal of 3 sys­tem eigen­func­tions for dis­tri­b­u­tion B, as shown in fig­ure 6.10.

It fol­lows that the sym­metriza­tion re­quire­ment re­duces the num­ber of eigen­func­tions for dis­tri­b­u­tion A, with 2 par­ti­cles in the ground state, from 9 to 3. How­ever, it re­duces the eigen­func­tions for dis­tri­b­u­tion B, with 1 par­ti­cle in the ground state, from 12 to 3. Not only does the sym­metriza­tion re­quire­ment re­duce the num­ber of en­ergy eigen­func­tions, but it also tends to shift the bal­ance to­wards eigen­func­tions that have more par­ti­cles in the ground state.

And so, if the sys­tem size is in­creased un­der con­di­tions of Bose-Ein­stein con­den­sa­tion, it turns out that there are as­tro­nom­i­cally more sys­tem eigen­func­tions for an en­ergy dis­tri­b­u­tion that keeps a fi­nite num­ber of bosons in the ground state than for any­thing else.

It may be noted from com­par­ing fig­ures 6.7 and 6.8 with 6.9 and 6.10 that any en­ergy dis­tri­b­u­tion that is phys­i­cally pos­si­ble for dis­tin­guish­able par­ti­cles is just as pos­si­ble for iden­ti­cal bosons. Bose-Ein­stein con­den­sa­tion does not oc­cur be­cause the physics says it must, but be­cause there are so gi­gan­ti­cally more sys­tem eigen­func­tions that have a fi­nite frac­tion of bosons in the ground state than ones that do not.

It may also be noted that the re­duc­tion in the num­ber of sys­tem en­ergy eigen­func­tions for bosons is be­lieved to be an im­por­tant fac­tor in su­per­flu­id­ity. It elim­i­nates low-en­ergy eigen­func­tions that can­not be in­ter­preted as phonons, trav­el­ing par­ti­cle wave so­lu­tions, [18,39]. The lack of al­ter­nate eigen­func­tions leaves no mech­a­nism for the trav­el­ing par­ti­cles to get scat­tered by small ef­fects.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

En­ergy dis­tri­b­u­tions de­scribe how many par­ti­cles are found at each en­ergy level.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

For macro­scopic sys­tems, one par­tic­u­lar en­ergy dis­tri­b­u­tion has as­tro­nom­i­cally more en­ergy eigen­func­tions than any other one.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

That en­ergy dis­tri­b­u­tion is the only one that is ever ob­served.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Un­der con­di­tions of Bose-Ein­stein con­den­sa­tion, the ob­served dis­tri­b­u­tion has a fi­nite frac­tion of bosons in the ground state.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

This hap­pens be­cause the sys­tem eigen­func­tion count for bosons pro­motes it.