6.2 The Single-Particle States

As the previous section noted, the objective is to understand systems of noninteracting particles stuck in a closed, impenetrable, box. To do so, the key question is what are the single-particle quantum states, or energy eigenfunctions, for the particles. They will be discussed in this section.

The box will be taken to be rectangular, with its sides aligned with the coordinate axes. The lengths of the sides of the box will be indicated by $\ell_x$, $\ell_y$, and $\ell_z$ respectively.

The single-particle energy eigenfunctions for such a box were derived in chapter 3.5 under the guise of a pipe with a rectangular cross section. The single-particle energy eigenfunctions are:

$$\fbox{$\displaystyle \pp{n_xn_yn_z}/{\skew0\vec r}/// ... ...}{{\cal V}}}\; \sin (k_x x) \sin (k_y y) \sin (k_z z) $} %$$ (6.2)

Here ${\cal V}=\ell_x\ell_y\ell_z$ is the volume of the box. The “wave numbers” $k_x$, $k_y$, and $k_z$ take the values:

$$\fbox{$\displaystyle k_x = n_x \frac{\pi}{\ell_x}\quad ... ...frac{\pi}{\ell_y}\quad k_z = n_z \frac{\pi}{\ell_z} $} %$$ (6.3)

where $n_x$, $n_y$, and $n_z$ are natural numbers. Each set of three natural numbers $n_x,n_y,n_z$ gives one single-particle eigenfunction. In particular, the single-particle eigenfunction of lowest energy is $\pp{111}////$, having $n_x=n_y=n_z=1$.

Figure 6.1: Allowed wave number vectors, left, and energy spectrum, right.

However, the precise form of the eigenfunctions is not really that important here. What is important is how many there are and what energy they have. That information can be summarized by plotting the allowed wave numbers in a $k_x,k_y,k_z$ axis system. Such a plot is shown in the left half of figure 6.1.

Each point in this “wave number space” corresponds to one spatial single-particle state. The coordinates $k_x$, $k_y$, and $k_z$ give the wave numbers in the three spatial directions. In addition, the distance $k$ from the origin indicates the single-particle energy. More precisely, the single particle energy is

$$\fbox{$\displaystyle {\vphantom' E}^{\rm p}= \frac{\hbar... ... k^2 \qquad k \equiv \sqrt{k_x^2 + k_y^2 + k_z^2} $} %$$ (6.4)

The energy is therefore just a constant times the square of this distance. (The above expression for the energy can be verified by applying the kinetic energy operator on the given single-particle wave function.)

One more point must be made. The single-particle energy eigenfunctions described above are spatial states. Particles with nonzero spin, which includes all fermions, can additionally have different spin in whatever is chosen to be the $z$-direction. In particular, for fermions with spin $\leavevmode\kern.03em \raise.7ex\hbox{\the\scriptfont0 1}\kern-.2em /\kern-.2em\lower.4ex\hbox{\the\scriptfont0 2}\kern.05em$, including electrons, there is a “spin-up” and a “spin-down” version of each spatial energy eigenfunction:

$$\begin{eqnarray*} \pp{n_xn_yn_z,\frac12}/{\skew0\vec r}//z/ & = & \sqrt{\fra... ...cal V}}}\; \sin(k_xx) \sin(k_yy) \sin(k_zz) \;{\downarrow}(S_z) \end{eqnarray*}$$

That means that each point in the wave number space figure 6.1 stands for two single-particle states, not just one.

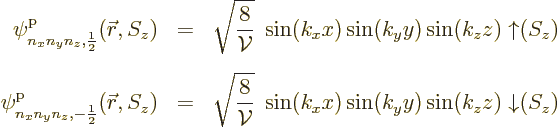
In general, if the particles have spin $s$, each point in wave number space corresponds to $2s+1$ different single-particle states. However, photons are an exception to this rule. Photons have spin $s=1$ but each spatial state corresponds to only 2 single-particle states, not 3. (That is related to the fact that the spin angular momentum of a photon in the direction of motion can only be $\hbar$ or $-\hbar$, not 0. And that is in turn related to the fact that the electromagnetic field cannot have a component in the direction of motion. If you are curious, see addendum {A.19.6} for more.)

Key Points

Each single particle state is characterized by a set of three “wave numbers” $k_x$, $k_y$, and $k_z$.

Each point in the “wave number space” figure 6.1 corresponds to one specific spatial single-particle state.

The distance of the point from the origin is a measure of the energy of the single-particle state.

In the presence of nonzero particle spin $s$, each point in wave number space corresponds to $2s+1$ separate single-particle states that differ in the spin in the chosen $z$-direction. For photons, make that $2s$ instead of $2s+1$.