|
|
|
|
|
Next: 4. Single-Particle Systems |
|
This section demonstrates the general procedure for analyzing quantum systems using a very elementary example. The system to be studied is that of a particle, say an electron, confined to the inside of a narrow pipe with sealed ends. This example will be studied in some detail, since if you understand it thoroughly, it becomes much easier not to get lost in the more advanced examples of quantum mechanics discussed later. And as the final subsection 3.5.9 shows, as well as much of chapter 6, the particle in a pipe is really quite interesting despite its simplicity.
The system to be analyzed is shown in figure 3.4 as it would appear in classical nonquantum physics.
A particle is bouncing around between the two ends of a pipe. It is assumed that there is no friction, so the particle will keep bouncing back and forward forever. (Friction is a macroscopic effect that has no place in the sort of quantum-scale systems analyzed here.) Typically, classical physics draws the particles that it describes as little spheres, so that is what figure 3.4 shows.
The actual quantum system to be analyzed is shown in figure 3.5.
A particle like an electron has no (known) specific shape or size, but
it does have a wave function blob.
So in quantum
mechanics the equivalent of a particle bouncing around is a wave
function blob bouncing around between the ends of the pipe.
Please do not ask what this impenetrable pipe is made off. It is obviously a crude idealization. You could imagine that the electron is a valence electron in a very tiny bar of copper. In that case the pipe walls would correspond to the surface of the copper bar, and it is assumed that the electron cannot get off the bar.
But of course, a copper bar would have nuclei, and other electrons, and the analysis here does not consider those. So maybe it is better to think of the particle as being a lone helium atom stuck inside a carbon nanotube.
Key Points
- An idealized problem of a particle bouncing about in a pipe will be considered.
The first step in the solution process is to describe the problem
mathematically. To do so, an ![]() -
-![]() .
.
To make the problem as easy to solve as possible, it will be assumed
that the only position coordinate that exists is the longitudinal
position ![]()
![]()
![]()
Key Points
- The only position coordinate to be considered for now is
.
- The notations have been defined.
To analyze a quantum system you must find the Hamiltonian. The Hamiltonian is the total energy operator, equal to the sum of kinetic plus potential energy.
The potential energy ![]()
Next, the kinetic energy operator ![]()
Since the potential energy is zero, the Hamiltonian ![]()
Key Points
- The one-dimensional Hamiltonian (3.13) has been written down.
With the Hamiltonian ![]()
Substituting the Hamiltonian for the pipe as found in the previous
subsection, the eigenvalue problem is:
The problem is not complete yet. These problems also need so called
boundary conditions
, conditions that say what happens
at the ends of the ![]()
![]()
Key Points
- The Hamiltonian eigenvalue problem (3.14)has been found.
- It also includes the boundary conditions (3.15).
The previous section found the Hamiltonian eigenvalue problem to be:
differentialbecause it has a derivative in it, and
ordinarysince there are no derivatives with respect to variables other than
If you do not know how to solve ordinary differential equations, it is
no big deal. The best way is usually to look them up anyway. The
equation above can be found in most mathematical table books, e.g.
[41, item 19.7]. According to what it says there, (with
changes in notation), if you assume that the energy ![]()
As far as the ordinary differential equation is concerned, the
constants ![]()
![]()
![]()
![]()
![]()
![]()
![]()
The second boundary condition, that ![]()
![]()
![]()
![]()
![]() ,
,
Everything was done right. So the problem must be the initial assumption that the energy is negative. Apparently, the energy cannot be negative. This can be understood from the fact that for this particle, the energy is all kinetic energy. Classical physics would say that the kinetic energy cannot be negative because it is proportional to the square of the velocity. You now see that quantum mechanics agrees that the kinetic energy cannot be negative, but says it is because of the boundary conditions on the wave function.
Try again, but now assume that the energy ![]()
Note that classically, it is perfectly OK for the energy to be zero: it would simply mean that the particle is sitting in the pipe at rest. But in quantum mechanics, zero kinetic energy is not acceptable, and it all has to do with Heisenberg's uncertainty principle. Since the particle is restricted to the inside of the pipe, its position is constrained, and so the uncertainty principle requires that the linear momentum must be uncertain. Uncertain momentum cannot be zero momentum; measurements will show a range of values for the momentum of the particle, implying that it is in motion and therefore has kinetic energy.
Try, try again. The only possibility left is that the energy ![]()

The boundary condition that ![]()
![]()
![]()
![]()
Each of these possibilities gives one solution ![]() .
.![]()
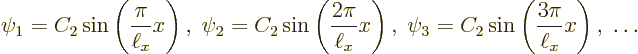
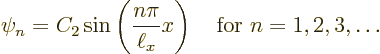
Let’s check the solutions. Clearly each is zero when ![]()
![]()
![]()
![]()
![]() .
.
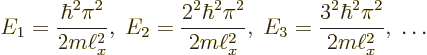
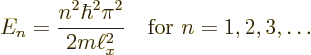
There is one more condition that must be satisfied:
each solution must be normalized so that the total probability
of finding the particle integrated over all possible positions
is 1 (certainty). That requires:
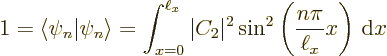

Summarizing the results of this subsection, there is not just one
energy eigenfunction and corresponding eigenvalue, but an infinite set
of them:
Key Points
- After a lot of grinding mathematics armed with table books, the energy eigenfunctions and eigenvalues have finally been found
- There are infinitely many of them.
- They are as listed in (3.17) above. The first few are also written out explicitly in (3.16).
Write down eigenfunction number 6.
Write down eigenvalue number 6.
This subsection discusses the energy that the particle in the pipe can
have. It was already discovered in the previous subsection that the
particle cannot have negative energy, nor zero energy. In fact,
according to the orthodox interpretation, the only values that the
total energy of the particle can take are the energy eigenvalues
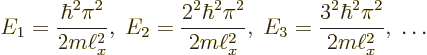
Energy values are typically shown graphically in the form of an
energy spectrum
, as in figure 3.7.
Energy is plotted upwards, so the vertical height of each energy level
indicates the amount of energy it has. To the right of each energy
level, the solution counter, or quantum number
, ![]()
Classically, the total energy of the particle can have any nonnegative
value. But according to quantum mechanics, that is not true: the
total energy must be one of the levels shown in the energy spectrum
figure
3.7. It should be noted that for a macroscopic
particle, you would not know the difference; the spacing between the
energy levels is macroscopically very fine, since Planck's constant
![]()
Another point: at absolute zero temperature, the particle will be
stuck in the lowest possible energy level, ![]()
![]()
![]()
![]()
![]() ,
,ground state.
Classically you would expect that at
absolute zero the particle has no kinetic energy, so zero total
energy. But quantum mechanics does not allow it. Heisenberg's
principle requires some momentum, hence kinetic energy to remain for a
confined particle even at zero temperature.
Key Points
- Energy values can be shown as an energy spectrum.
- The possible energy levels are discrete.
- But for a macroscopic particle, they are extremely close together.
- The ground state of lowest energy has nonzero kinetic energy.
Plug the mass of an electron, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Just for fun, plug macroscopic values, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
What is the eigenfunction number, or quantum number, ![]()
![]()
![]()
![]()
![]()
This subsection discusses the one-dimensional energy eigenfunctions of
the particle in the pipe. The solution of subsection 3.5.5
found them to be:
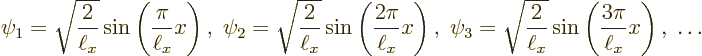
The first one to look at is the ground state eigenfunction
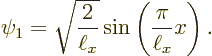
It is seen that in the ground state, the particle is much more likely to be found somewhere in the middle of the pipe than close to the ends.
Figure 3.9 shows the two next lowest energy states
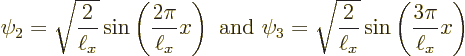
Needless to say, none of those energy states looks at all like the wave function blob bouncing around in figure 3.5. Moreover, it turns out that energy eigenstates are stationary states: the probabilities shown in figures 3.8 and 3.9 do not change with time.
In order to describe a localized wave function blob bouncing around, states of different energy must be combined. It will take until chapter 7.11.4 before the analytical tools to do so have been described. For now, the discussion must remain restricted to just finding the energy levels. And these are important enough by themselves anyway, sufficient for many practical applications of quantum mechanics.
Key Points
- In the energy eigenfunctions, the particle is not localized to within any particular small region of the pipe.
- In general there are regions where the particle may be found separated by regions in which there is little chance to find the particle.
- The higher the energy level, the more such regions there are.
So how does, say, the one-dimensional eigenstate ![]()
Generalizing the results above, for eigenfunction ![]() ,
,![]() ,
,
If you are up to a trick question, consider the following. There are no forces inside the pipe, so the particle has to keep moving until it hits an end of the pipe, then reflect backward until it hits the other side and so on. So, it has to cross the center of the pipe regularly. But in the energy eigenstate ![]() ,
,
The solution for the particle stuck in a pipe that was obtained in the
previous subsections cheated. It pretended that there was only one
spatial coordinate ![]() .
.
Fortunately, it turns out that you can fix up the problem pretty
easily if you assume that the pipe has a square cross section. There
is a way of combining one-dimensional solutions for all three coordinates
into full three-dimensional solutions. This is called the
separation of variables
idea: Solve each of the three
variables ![]() ,
,![]() ,
,![]()
The full coordinate system for the problem is shown in figure
3.10: in addition to the ![]() -
-![]() -
-![]() -
-
Now recall the one-dimensional solutions that were obtained assuming there
is just an ![]() -
-
to
keep them apart from any solutions for ![]()
![]()
![]() :
:
 |
(3.18) |
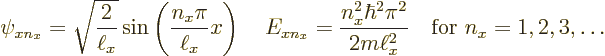 |
(3.19) |
Since it is assumed that the cross section of the pipe is square or
rectangular of dimensions ![]()
![]()
![]() ,
,![]()
![]()
![]()
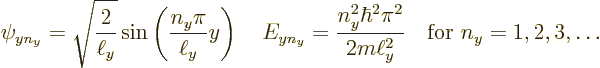 |
(3.20) |
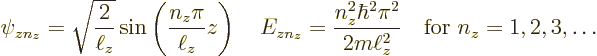 |
(3.21) |
Now it turns out, {D.11}, that the full three-dimensional
problem has eigenfunctions ![]()
quantum numbersof the eigenfunction.
Further, the energy eigenvalues ![]()
For example, the ground state of lowest energy occurs when all three
quantum numbers are lowest, ![]()
![]()
![]()
![]()
![]()
![]()
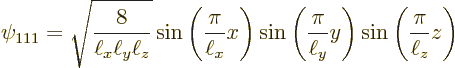 |
(3.24) |
The ground state energy is:
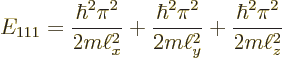 |
(3.25) |
The next two lowest energy levels occur for ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1![]()
![]() 2
2![]()
![]()
![]()
![]() 1
1
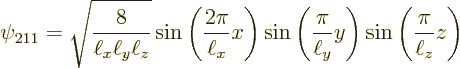 |
(3.26) |
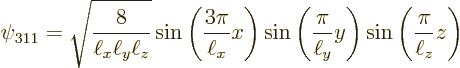 |
(3.27) |
 |
(3.28) |
Key Points
- Three-dimensional energy eigenfunctions can be found as products of one-dimensional ones.
- Three-dimensional energies can be found as sums of one-dimensional ones.
- Example three-dimensional eigenstates have been shown.
If the cross section dimensions ![]()
![]()
![]()
![]()
![]() ?
?![]()
![]() ,
,
At what ratio of ![]()
![]()
![]()
![]()
![]() ?
?
Shade the regions where the particle is likely to be found in the ![]()
Normally, motion in physics occurs in three dimensions. Even in a narrow pipe, in classical physics a point particle of zero size would be able to move in all three directions. But in quantum mechanics, if the pipe gets very narrow, the motion becomes truly one-dimensional.
To understand why, the first problem that must be addressed is what
motion
means in the first place, because normally
motion is defined as change in position, and in quantum mechanics
particles do not have a well-defined position.
Consider the particle in the ground state of lowest energy, shown in figure 3.11. This is one boring state; the picture never changes. You might be surprised by that; after all, it was found that the ground state has energy, and it is all kinetic energy. If the particle has kinetic energy, should not the positions where the particle is likely to be found change with time?
The answer is no; kinetic energy is not directly related to changes in likely positions of a particle; that is only an approximation valid for macroscopic systems. It is not necessarily true for quantum-scale systems, certainly not if they are in the ground state. Like it or not, in quantum mechanics kinetic energy is second-order derivatives of the wave function, and nothing else.
Next, as already pointed out, all the other energy eigenstates, like those in figure 3.12, have the same boring property of not changing with time.
Things only become somewhat interesting when you combine states of
different energy. As the simplest possible example, consider the
possibility that the particle has the wave function:
In chapter 7.1 it will be found that for nonzero
times, the wave function of this particle is given by
You would not yet want to call the particle localized, but at least
the locations where the particle can be found are now bouncing back
and forwards between the ends of the pipe. And if you add additional
wave functions ![]() ,
,![]() ,
,
But if you look closer at figure 3.13, you will note that
the wave function blob does not move at all in the ![]() -
-![]()
![]() ,
,![]() -
-
But there is a catch, and it has to do with the required energy.
According to the previous section, the kinetic energy in the
![]() -
-

The result is that absolutely nothing interesting goes on in the
![]() -
-![]() -
-![]() -
-![]() ,
,
If the pipe is also narrow in the ![]() -
-![]() -
-![]() -
-![]() -
-
An isolated atom can be regarded as an example of a quantum dot; the electrons are confined to a small region around the nucleus and will be at a single energy level unless they are given a considerable amount of energy. But note that when people talk about quantum confinement, they are normally talking about semi-conductors, for which similar effects occur at significantly larger scales, maybe tens of times as large, making them much easier to manufacture. An actual quantum dot is often referred to as an “artificial atom”, and has similar properties as a real atom.
It may give you a rough idea of all the interesting things you can do in nanotechnology when you restrict the motion of particles, in particular of electrons, in various directions. You truly change the dimensionality of the normal three-dimensional world into a lower dimensional one. Only quantum mechanics can explain why, by making the energy levels discrete instead of continuously varying. And the lower dimensional worlds can have your choice of topology (a ring, a letter 8, a sphere, a cylinder, a Möbius strip?, ...,) to make things really exciting.
Key Points
- Quantum mechanics allows you to create lower-dimensional worlds for particles.