| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
2.4 Operators
This section defines operators, which are a generalization of
matrices. Operators are the principal components of quantum
mechanics.
In a finite number of dimensions, a matrix A can transform any arbitrary vector 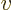 into a different
vector
into a different
vector 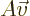 :
:
Similarly, an operator transforms a function into another function:
Some simple examples of operators:
Note that a hat is often used to indicate operators; for example,  is the symbol for the operator that corresponds to multiplying by
is the symbol for the operator that corresponds to multiplying by
 . If it is clear that something is an operator, such as
. If it is clear that something is an operator, such as
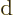

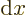 , no hat will be used.
, no hat will be used.
It should really be noted that the operators that you are interested
in in quantum mechanics are linear
operators. If you
increase a function  by a factor,
by a factor, 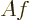 increases by that same
factor. Also, for any two functions
increases by that same
factor. Also, for any two functions  and
and  ,
,  will
be
will
be 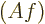 +
+ 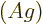 . For example, differentiation is a linear
operator:
. For example, differentiation is a linear
operator:
Squaring is not a linear operator:
However, it is not something to really worry about. You will not find
a single nonlinear operator in the rest of this entire book.
Key Points

- Matrices turn vectors into other vectors.

- Operators turn functions into other functions.
2.4 Review Questions
-
1.
-
So what is the result if the operator 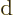

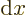 is applied to the function
is applied to the function 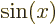 ?
?
Solution mathops-a
-
2.
-
If, say, 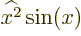 is simply the function
is simply the function 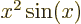 , then what is the difference between
, then what is the difference between 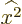 and
and 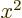 ?
?
Solution mathops-b
-
3.
-
A less self-evident operator than the above examples is a translation operator like 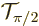 that translates the graph of a function towards the left by an amount
that translates the graph of a function towards the left by an amount 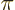
 2:
2: 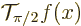

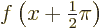 . (Curiously enough, translation operators turn out to be responsible for the law of conservation of momentum.) Show that
. (Curiously enough, translation operators turn out to be responsible for the law of conservation of momentum.) Show that 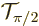 turns
turns 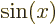 into
into 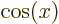 .
.
Solution mathops-c
-
4.
-
The inversion, or parity, operator  turns
turns  into
into 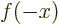 . (It plays a part in the question to what extent physics looks the same when seen in the mirror.) Show that
. (It plays a part in the question to what extent physics looks the same when seen in the mirror.) Show that  leaves
leaves 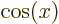 unchanged, but turns
unchanged, but turns 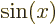 into
into 
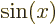 .
.
Solution mathops-d
![]()
![]() :
:
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.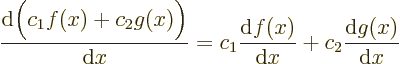
![]()
![]()
![]()
![]() ?
?![]()
![]() ,
,![]()
![]() ?
?![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.