|
|
|
|
|
Next: 2.4 Operators |
|
The dot product of vectors is an important tool. It makes it possible to find the length of a vector, by multiplying the vector by itself and taking the square root. It is also used to check if two vectors are orthogonal: if their dot product is zero, they are. In this subsection, the dot product is defined for complex vectors and functions.
The usual dot product of two vectors ![]()
![]()
![]()
is always equal.) Figure 2.6 shows multiplied components using equal colors.
Note the use of numeric subscripts, ![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ;
;
summation symbol.
The length of a vector ![]() ,
,![]()
![]() ,
,
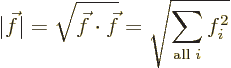
Therefore, it is necessary to use a generalized “inner product” for complex vectors, which puts a complex
conjugate on the first vector:
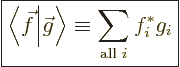 |
(2.7) |
The length of a nonzero vector is now always a positive number:
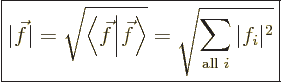 |
(2.8) |
Physicists take the inner product bracket
verbally
apart as
![\begin{displaymath}
\begin{array}{ccc}
{\left\langle\vec f\hspace{0.3pt}\right...
...ox{bra} & \makebox[0pt][l]{/}\mbox{c} & \mbox{ket}
\end{array}\end{displaymath}](img250.gif)
The inner product of functions is defined in exactly the same way as for
vectors, by multiplying values at the same ![]() -
-![]()
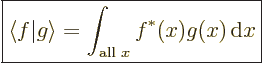 |
(2.9) |
The equivalent of the length of a vector is in the case of a function
called its “norm:”
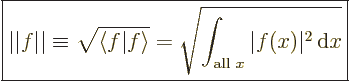 |
(2.10) |
A vector or function is called “normalized” if its length or norm is one:
| (2.11) |
if and only if.)
Two vectors, or two functions, ![]()
![]() ,
,
| (2.12) |
Sets of vectors or functions that are all
orthogonalis often used instead. This document will refer to them correctly as being orthonormal.
So, a set of functions or vectors ![]()
Key Points
- For complex vectors and functions, the normal dot product becomes the inner product.
- To take an inner product of vectors,
- take complex conjugates of the components of the first vector;
- multiply corresponding components of the two vectors together;
- sum these products.
- To take an inner product of functions,
- take the complex conjugate of the first function;
- multiply the two functions;
- integrate the product function.
- To find the length of a vector, take the inner product of the vector with itself, and then a square root.
- To find the norm of a function, take the inner product of the function with itself, and then a square root.
- A pair of vectors, or a pair of functions, is orthogonal if their inner product is zero.
- A set of vectors forms an orthonormal set if every one is orthogonal to all the rest, and every one is of unit length.
- A set of functions forms an orthonormal set if every one is orthogonal to all the rest, and every one is of unit norm.
Find the following inner product of the two vectors:
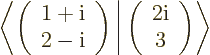
Find the length of the vector
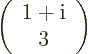
Find the inner product of the functions ![]()
![]()
![]()
![]()
![]()
Show that the functions ![]()
![]()
![]()
![]()
![]()
![]() .
.
Verify that ![]()
![]()
![]()
![]()
![]() ,
,
Verify that the most general multiple of ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() )
)![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
Show that the functions ![]()
![]()
![]()
![]()
![]()