|
|
|
|
|
Next: 13.3 Example Static Electromagnetic Fields |
|
Maxwell’s equations are commonly not covered in a typical engineering program. While these laws are not directly related to quantum mechanics, they do tend to pop up in nanotechnology. This section intends to give you some of the ideas. The description is based on the divergence and curl spatial derivative operators, and the related Gauss and Stokes theorems commonly found in calculus courses (Calculus III in the US system.)
Skipping the first equation for now, the second of Maxwell’s
equations comes directly out of the quantum mechanical description of
the previous section. Consider the expression for the magnetic field
![]()
derived
(guessed) there, (13.3).
If you take its divergence, (premultiply by ![]() )
)![]() ,
,
The first of Maxwell’s equations is a similar expression for the
electric field ![]() ,
,
What does it all mean? Well, the first thing to verify is that
Maxwell’s first equation is just a very clever way to write
Coulomb’s law for the electric field of a point charge. Consider
therefore an electric point charge of strength ![]() ,
,![]() ,
,![]()
![]()
![]() ;
;
Now watch what happens if you integrate both sides of Maxwell’s
first equation (13.5) over the interior of this
sphere. Starting with the right hand side, since the charge density
is the charge per unit volume, by definition its integral over the
volume is the charge ![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
Of course, all this raises the question, why bother? If Maxwell’s first equation is just a rewrite of Coulomb’s law, why not simply stick with Coulomb’s law in the first place? Well, to describe the electric field at a given point using Coulomb’s law requires you to consider every charge everywhere else. In contrast, Maxwell’s equation only involves local quantities at the given point, to wit, the derivatives of the local electric field and the local charge per unit volume. It so happens that in numerical or analytical work, most of the time it is much more convenient to deal with local quantities, even if those are derivatives, than with global ones.
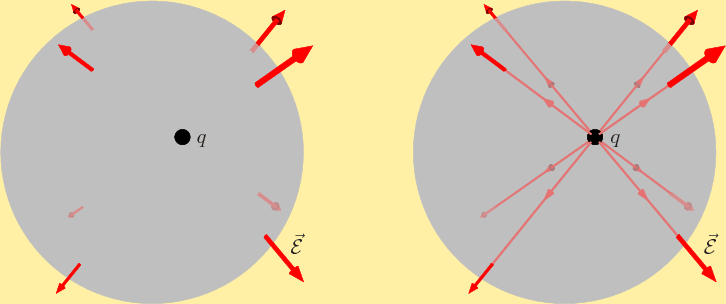 |
Of course, you can also integrate Maxwell’s first equation over
more general regions than a sphere centered around a charge. For
example figure 13.2 shows a sphere with an off-center
charge. But the electric field strength is no longer constant over
the surface, and divergence theorem now requires you to integrate the
component of the electric field normal to the surface over the
surface. Clearly, that does not have much intuitive meaning.
However, if you are willing to loosen up a bit on mathematical
preciseness, there is a better way to look at it. It is in terms of
the electric field lines
, the lines that everywhere
trace the direction of the electric field. The left figure in figure
13.2 shows the field lines through the selected points;
a single charge has radial field lines.
 |
Assume that you draw the field lines densely, more like figure 13.3 say, and moreover, that you make the number of field lines coming out of a charge proportional to the strength of that charge. In that case, the local density of field lines at a point becomes a measure of the strength of the electric field at that point, and in those terms, Maxwell’s integrated first equation says that the net number of field lines leaving a region is proportional to the net charge inside that region. That remains true when you add more charges inside the region. In that case the field lines will no longer be straight, but the net number going out will still be a measure of the net charge inside.
Now consider the question why Maxwell’s second equation says that the divergence of the magnetic field is zero. For the electric field you can shove, say, some electrons in the region to create a net negative charge, or you can shove in some ionized molecules to create a net positive charge. But the magnetic equivalents to such particles, called “magnetic monopoles”, being separate magnetic north pole particles or magnetic south pole particles, simply do not exist, {N.31}. It might appear that your bar magnet has a north pole and a south pole, but if you take it apart into little pieces, you do not end up with north pole pieces and south pole pieces. Each little piece by itself is still a little magnet, with equally strong north and south poles. The only reason the combined magnet seems to have a north pole is that all the microscopic magnets of which it consists have their north poles preferentially pointed in that direction.
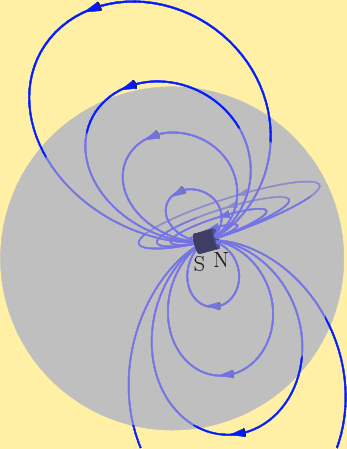 |
If all microscopic magnets have equal strength north and south poles,
then the same number of magnetic field lines that come out of the
north poles go back into the south poles, as figure 13.4
illustrates. So the net magnetic field lines leaving a given
region will be zero; whatever goes out comes back in. True, if you
enclose the north pole of a long bar magnet by an imaginary sphere,
you can get a pretty good magnetic approximation of the electrical
case of figure 13.1. But even then, if you look
inside the magnet where it sticks through the spherical
surface, the field lines will be found to go in towards the
north pole, instead of away from it. You see why Maxwell’s second
equation is also called absence of magnetic monopoles.
And why, say, electrons can have a net negative charge, but have zero
magnetic pole strength; their spin and orbital angular momenta produce
equally strong magnetic north and south poles, a magnetic
dipole
(di meaning two.)
You can get Maxwell’s third equation from the electric field
derived
in the previous section. If you take its
curl, (premultiply by ![]() )
)![]() ,
,![]()
curl,
rot.
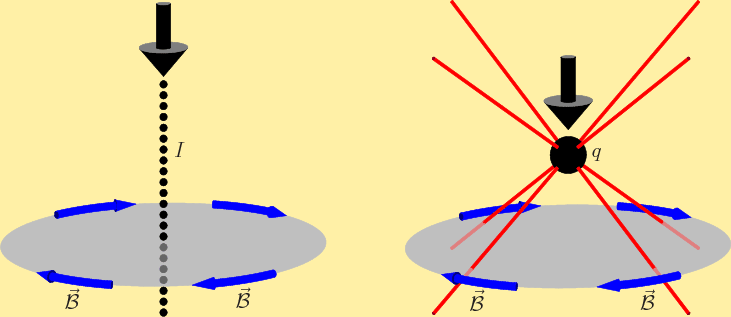
Now what does that one mean? Well, the first thing to verify in this case is that this is just a clever rewrite of Faraday's law of induction, governing electric power generation. Assume that you want to create a voltage to drive some load (a bulb or whatever, don’t worry what the load is, just how to get the voltage for it.) Just take a piece of copper wire and bend it into a circle, as shown in figure 13.5. If you can create a voltage difference between the ends of the wire you are in business; just hook your bulb or whatever to the ends of the wire and it will light up. But to get such a voltage, you will need an electric field as shown in figure 13.5 because the voltage difference between the ends is the integral of the electric field strength along the length of the wire. Now Stokes' theorem of calculus says that the electric field strength along the wire integrated over the length of the wire equals the integral of the curl of the electric field strength integrated over the inside of the wire, in other words over the imaginary translucent circle in figure 13.5. So to get the voltage, you need a nonzero curl of the electric field on the translucent circle. And Maxwell’s third equation above says that this means a time-varying magnetic field on the translucent circle. Moving the end of a strong magnet closer to the circle should do it, as suggested by figure 13.5. You better not make that a big bulb unless you you wrap the wire around a lot more times to form a spool, but anyway. {N.32}.
Maxwell’s fourth and final equation is a similar expression for
the curl of the magnetic field:
electric current density,the charge flowing per unit cross sectional area, and
 |
The big difference from the third equation is the appearance of the
current density ![]() .
.
The fact that a current creates a surrounding magnetic field was
already known as Ampere's law when Maxwell did his analysis. Maxwell
himself however added the time derivative of the electric field to the
equation to have the mathematics make sense. The problem was that the
divergence of any curl must be zero, and by itself, the divergence of
the current density in the right hand side of the fourth equation is
not zero. Just like the divergence of the electric field is
the net field lines coming out of a region per unit volume, the
divergence of the current density is the net current coming out. And
it is perfectly OK for a net charge to flow out of a region: it simply
reduces the charge remaining within the region by that amount. This
is expressed by the continuity equation:
In empty space, Maxwell’s equations simplify: there are no charges
so both the charge density ![]()
![]()
You can plug the above wave solution into Maxwell’s equations and so verify that it satisfies them all. With more effort and knowledge of Fourier analysis, you can show that they are the most general possible solutions that take this traveling wave form, and that any arbitrary solution is a combination of these waves (if all directions of the propagation direction and of the electric field relative to it, are included.)
The point is that the waves travel with the speed ![]() .
.![]()
It was a great victory of mathematical analysis. Long ago, the Greeks had tried to use mathematics to make guesses about the physical world, and it was an abysmal failure. You do not want to hear about it. Only when the Renaissance started measuring how nature really works, the correct laws were discovered for people like Newton and others to put into mathematical form. But here, Maxwell successfully amends Ampere's measured law, just because the mathematics did not make sense. Moreover, by deriving how fast electromagnetic waves move, he discovers the very fundamental nature of the then mystifying physical phenomenon humans call light.
For those with a knowledge of partial differential equations, separate wave equations for the electric and magnetic fields and their potentials are derived in addendum {A.37}.
An electromagnetic field obviously contains energy; that is how the
sun transports heat to our planet. The electromagnetic energy within
an otherwise empty volume ![]()
But at least the result can be made plausible. First note that the
time derivative of the energy above can be written as
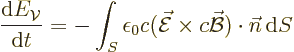
Now suppose you have a finite amount of radiation in otherwise empty
space. If the amount of radiation is finite, the field should
disappear at infinity. So, taking the volume to be all of space, the
integral in the right hand side above will be zero. So ![]()
![]()
![]()
![]()
For an arbitrary volume ![]() ,
,
You will usually not find Maxwell’s equations in the exact form
described here. To explain what is going on inside materials, you
would have to account for the electric and magnetic fields of every
electron and proton (and neutron!) of the material. That is just an
impossible task, so physicists have developed ways to average away all
those effects by messing with Maxwell’s equations. But then the
messed-up ![]()
![]()
![]() .
.![]()
electric flux density
![]() ,
,the auxiliary field
. And
they define many other symbols, and even refer to the auxiliary field
as being the magnetic field, all to keep engineers out of
nanotechnology. Don’t let them! When you need to understand the
messed-up Maxwell’s equations, Wikipedia has a list of the
countless definitions.