13.3 Example Static Electromagnetic Fields

In this section, some basic solutions of Maxwell’s equations are described. They will be of interest in addendum {A.36} for understanding relativistic effects on the hydrogen atom (though certainly not essential). They are also of considerable practical importance for a lot of nonquantum applications.

It is assumed throughout this subsection that the electric and magnetic fields do not change with time. All solutions also assume that the ambient medium is vacuum.

Table 13.1: Elecromagnetics I: Fundamental equations and basic solutions.

Table 13.2: Elecromagnetics II: Electromagnetostatic solutions.

For easy reference, Maxwell’s equations and various results to be obtained in this section are collected together in tables 13.1 and 13.2. While the existence of magnetic monopoles is unverified, it is often convenient to compute as if they do exist. It allows you to apply ideas from the electric field to the magnetic field and vice-versa. So, the tables include magnetic monopoles with strength $q_m$, in addition to electric charges with strength $q$, and a magnetic current density $\vec\jmath_m$ in addition to an electric current density $\vec\jmath$. The table uses the permittivity of space $\epsilon_0$ and the speed of light $c$ as basic physical constants; the permeability of space $\mu_0=1/\epsilon_0c^2$ is just an annoyance in quantum mechanics and is avoided. The table has been written in terms of $c\skew2\vec{\cal B}$ and $\vec\jmath_m/c$ because in terms of those combinations Maxwell’s equations have a very pleasing symmetry. It allows you to easily convert between expressions for the electric and magnetic fields. You wish that physicists would have defined the magnetic field as $c\skew2\vec{\cal B}$ instead of $\skew2\vec{\cal B}$ in SI units, but no such luck.

13.3.1 Point charge at the origin

A point charge is a charge concentrated at a single point. It is a very good model for the electric field of the nucleus of an atom, since the nucleus is so small compared to the atom. A point charge of strength $q$ located at the origin has a charge density

$$\mbox{point charge at the origin:}\quad \rho({\skew0\vec r}) = q \delta^3({\skew0\vec r})$$ (13.13)

where $\delta^3({\skew0\vec r})$ is the three dimensional delta function. A delta function is a spike at a single point that integrates to one, so the charge density above integrates to the total charge $q$.

The electric field lines of a point charge are radially outward from the charge; see for example figure 13.3 in the previous subsection. According to Coulomb’s law, the electric field of a point charge is

$$\fbox{$\displaystyle \mbox{electric field of a point cha... ...c{\cal E}= \frac{q}{4\pi\epsilon_0r^2} {\hat\imath}_r $} %$$ (13.14)

where $r$ is the distance from the charge, ${\hat\imath}_r$ is the unit vector pointing straight away from the charge, and $\epsilon_0$ = 8.85 10$\POW9,{-12}$ C$\POW9,{2}$/J m is the permittivity of space. Now for static electric charges the electric field is minus the gradient of a potential $\varphi$,

$$\skew3\vec{\cal E}= - \nabla\varphi \qquad \nabla \equi... ...\partial}{\partial y} + {\hat k}\frac{\partial}{\partial z}$$

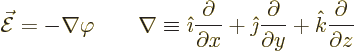
In everyday terms the potential $\varphi$ is called the “voltage.” It follows by integration of the electric field strength with respect to $r$ that the potential of a point charge is

$$\fbox{$\displaystyle \mbox{electric potential of a point charge:}\quad \varphi=\frac{q}{4\pi\epsilon_0r} $} %$$ (13.15)

Multiply by $-e$ and you get the potential energy $V$ of an electron in the field of the point charge. That was used in writing the Hamiltonians of the hydrogen and heavier atoms.

Delta functions are often not that easy to work with analytically, since they are infinite and infinity is a tricky mathematical thing. It is often easier to do the mathematics by assuming that the charge is spread out over a small sphere of radius $\varepsilon$, rather than concentrated at a single point. If it is assumed that the charge distribution is uniform within the radius $\varepsilon$, then it is

$$\mbox{spherical charge around the origin:}\quad \rho = ... ...aystyle 0 &\mbox{if } r > \varepsilon \end{array} \right.$$ (13.16)

Since the charge density is the charge per unit volume, the charge density times the volume $\frac43\pi\varepsilon^3$ of the little sphere that holds it must be the total charge $q$. The expression above makes it so.

Figure 13.7: Electric field and potential of a charge that is distributed uniformly within a small sphere. The dotted lines indicate the values for a point charge.

Figure 13.7 shows that outside the region with charge, the electric field and potential are exactly like those of a point charge with the same net charge $q$. But inside the region of charge distribution, the electric field varies linearly with radius, and becomes zero at the center. It is just like the gravity of earth: going above the surface of the earth out into space, gravity decreases like $1/r^2$ if $r$ is the distance from the center of the earth. But if you go down below the surface of the earth, gravity decreases also and becomes zero at the center of the earth. If you want, you can derive the electric field of the spherical charge from Maxwell’s first equation; it goes much in the same way that Coulomb’s law was derived from it in the previous section.

If magnetic monopoles exist, they would create a magnetic field much like an electric charge creates an electric field. As table 13.1 shows, the only difference is the square of the speed of light $c$ popping up in the expressions. (And that is really just a matter of definitions, anyway.) In real life, these expressions give an approximation for the magnetic field near the north or south pole of a very long thin magnet as long as you do not look inside the magnet.

Figure 13.8: Electric field of a two-dimensional line charge.

A homogeneous distribution of charges along an infinite straight line is called a line charge. As shown in figure 13.8, it creates a two-dimensional field in the planes normal to the line. The line charge becomes a point charge within such a plane. The expression for the field of a line charge can be derived in much the same way as Coulomb’s law was derived for a three-dimensional point charge in the previous section. In particular, where that derivation surrounded the point charge by a spherical surface, surround the line charge by a cylinder. (Or by a circle, if you want to think of it in two dimensions.) The resulting expressions are given in table 13.1; they are in terms of the charge per unit length of the line $q'$. Note that in this section a prime is used to indicate that a quantity is per unit length.

13.3.2 Dipoles

A point charge can describe a single charged particle like an atom nucleus or electron. But much of the time in physics, you are dealing with neutral atoms or molecules. For those, the net charge is zero. The simplest model for a system with zero net charge is called the “dipole.” It is simply a combination of a positive point charge $q$ and a negative one $-q$, making the net charge zero.

Figure 13.9: Field lines of a vertical electric dipole.

Figure 13.9 shows an example of a dipole in which the positive charge is straight above the negative one. Note the distinctive egg shape of the biggest electric field lines. The “electric dipole moment” $\vec\wp$ is defined as the product of the charge strength $q$ times the connecting vector from negative to positive charge:

$$\mbox{electric dipole moment:}\quad \vec\wp = q ({\skew0\vec r}_\oplus-{\skew0\vec r}_\ominus) %$$ (13.17)

where ${\skew0\vec r}_\oplus$ and ${\skew0\vec r}_\ominus$ are the positions of the positive and negative charges respectively.

The potential of a dipole is simply the sum of the potentials of the two charges:

$$\mbox{potential of an electric dipole:}\quad \varphi = \... ...frac{1}{\vert{\skew0\vec r}-{\skew0\vec r}_{\ominus}\vert} %$$ (13.18)

Note that to convert the expressions for a charge at the origin to one not at the origin, you need to use the position vector measured from the location of the charge.

The electric field of the dipole can be found from either taking minus the gradient of the potential above, or from adding the fields of the individual point charges, and is

$$\mbox{field of an electric dipole:}\quad \skew3\vec{\cal E... ...nus}}{\vert{\skew0\vec r}-{\skew0\vec r}_{\ominus}\vert^3} %$$ (13.19)

To obtain that result from taking the the gradient of the potential, remember the following important formula for the gradient of $\vert{\skew0\vec r}-{\skew0\vec r}_0\vert^n$ with $n$ an arbitrary power:

$$\fbox{$\displaystyle \frac{\partial\vert{\skew0\vec r}-{... ...vec r}_0\vert^{n-2} ({\skew0\vec r}-{\skew0\vec r}_0) $} %$$ (13.20)

The first expression gives the gradient in index notation and the second gives it in vector form. The subscript on $\nabla$ merely indicates that the differentiation is with respect to ${\skew0\vec r}$, not ${\skew0\vec r}_0$. These formulae will be used routinely in this section. Using them, you can check that minus the gradient of the dipole potential does indeed give its electric field above.

Similar expressions apply for magnetic dipoles. The field outside a thin bar magnet can be approximated as a magnetic dipole, with the north and south poles of the magnet as the positive and negative magnetic point charges. The magnetic field lines are then just like the electric field lines in figure 13.9.

Figure 13.10: Electric field of a two-dimensional dipole.

Corresponding expressions can also be written down in two dimensions, for opposite charges distributed along parallel straight lines. Figure 13.10 gives an example. In two dimensions, all field lines are circles passing through both charges.

A particle like an electron has an electric charge and no known size. It can therefore be described as an ideal point charge. But an electron also has a magnetic moment: it acts as a magnet of zero size. Such a magnet of zero size will be referred to as an “ideal magnetic dipole.” More precisely, an ideal magnetic dipole is defined as the limit of a magnetic dipole when the two poles are brought vanishingly close together. Now if you just let the two poles approach each other without doing anything else, their opposite fields will begin to increasingly cancel each other, and there will be no field left when the poles are on top of each other. When you make the distance between the poles smaller, you also need to increase the strengths $q_m$ of the poles to ensure that the

$$\mbox{magnetic dipole moment:}\quad \vec\mu = q_m ({\skew0\vec r}_\oplus-{\skew0\vec r}_\ominus)$$ (13.21)

remains finite. So you can think of an ideal magnetic dipole as infinitely strong magnetic poles infinitely close together.

Figure 13.11: Field of an ideal magnetic dipole.

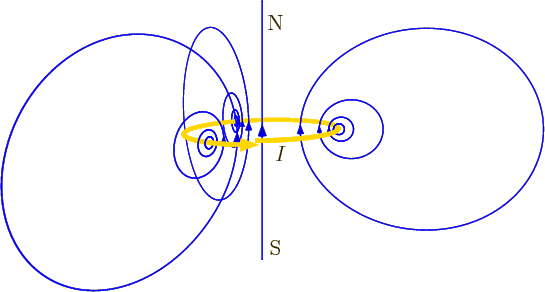
The field lines of a vertical ideal magnetic dipole are shown in figure 13.11. Their egg shape is in spherical coordinates described by, {D.74},

$$r = r_{\rm max} \sin^2\theta \qquad \phi = \mbox{constant} %$$ (13.22)

To find the magnetic field itself, start with the magnetic potential of a nonideal dipole,

$$\varphi_m = \frac{q_m}{4\pi\epsilon_0c^2} \left[ \frac{1... ...}{\vert{\skew0\vec r}-{\skew0\vec r}_{\ominus}\vert} \right]$$

Now take the negative pole at the origin, and allow the positive pole to approach it vanishingly close. Then the potential above takes the generic form

$$\varphi_m = f({\skew0\vec r}-{\skew0\vec r}_{\oplus}) - f(... ...ac{q_m}{4\pi\epsilon_0c^2} \frac{1}{\vert{\skew0\vec r}\vert}$$

Now according to the total differential of calculus, (or the multi-dimensional Taylor series theorem, or the definition of directional derivative), for small ${\skew0\vec r}_{\oplus}$ an expression of the form $f({\skew0\vec r}-{\skew0\vec r}_{\oplus})-f({\skew0\vec r})$ can be approximated as

$$f({\skew0\vec r}-{\skew0\vec r}_{\oplus}) - f({\skew0\vec ... ...\nabla f \quad\mbox{for}\quad {\skew0\vec r}_{\oplus} \to 0$$

From this the magnetic potential of an ideal dipole at the origin can be found by using the expression (13.20) for the gradient of $1/\vert{\skew0\vec r}\vert$ and then substituting the magnetic dipole strength $\vec\mu$ for $q_m{\skew0\vec r}_{\oplus}$. The result is

$$\mbox{potential of an ideal magnetic dipole:}\quad \varphi... ...{4\pi\epsilon_0c^2} \frac{\vec\mu\cdot{\skew0\vec r}}{r^3} %$$ (13.23)

The corresponding magnetic field can be found as minus the gradient of the potential, using again (13.20) and the fact that the gradient of $\vec\mu\cdot{\skew0\vec r}$ is just $\vec\mu$:

$$\skew2\vec{\cal B}= \frac{1}{4\pi\epsilon_0c^2} \frac{3(\vec\mu\cdot{\skew0\vec r}){\skew0\vec r}-\vec\mu r^2}{r^5} %$$ (13.24)

Similar expressions can be written down for ideal electric dipoles and in two-dimensions. They are listed in tables 13.1 and 13.2. (The delta functions will be discussed in the next subsection.)

Figure 13.12: Electric field of an almost ideal two-dimensional dipole.

Figure 13.12 shows an almost ideal two-dimensional electric dipole. The spacing between the charges has been reduced significantly compared to that in figure 13.10, and the strength of the charges has been increased. For two-dimensional ideal dipoles, the field lines in a cross-plane are circles that all touch each other at the dipole.

13.3.3 Arbitrary charge distributions

Modeling electric systems like atoms and molecules and their ions as singular point charges or dipoles is not very accurate, except in a detailed quantum solution. In a classical description, it is more reasonable to assume that the charges are “smeared out” over space into a distribution. In that case, the charges are described by the charge per unit volume, called the charge density $\rho$. The integral of the charge density over volume then gives the net charge,

$$q_{\rm region} = \int_{\rm region} \rho({\underline{\skew0\vec r}}) {\,\rm d}^3{\underline{\skew0\vec r}}$$ (13.25)

As far as the potential is concerned, each little piece $\rho({\underline{\skew0\vec r}}){\,\rm d}^3{\underline{\skew0\vec r}}$ of the charge distribution acts like a point charge at the point ${\underline{\skew0\vec r}}$. The expression for the potential of such a point charge is like that of a point charge at the origin, but with ${\skew0\vec r}$ replaced by ${\skew0\vec r}-{\underline{\skew0\vec r}}$. The total potential results from integrating over all the point charges. So, for a charge distribution,

$$\varphi({\skew0\vec r}) = \frac{1}{4\pi\epsilon_0} \int_{{... ...erline{\skew0\vec r}}){\,\rm d}^3{\underline{\skew0\vec r}} %$$ (13.26)

The electric field and similar expression for magnetic charge distributions and in two dimensions may be found in table 13.2

Note that when the integral expression for the potential is differentiated to find the electric field, as in table 13.2, the integrand becomes much more singular at the point of integration where ${\underline{\skew0\vec r}}={\skew0\vec r}$. This may be of importance in numerical work, where the more singular integrand can lead to larger errors. It may then be a better idea not to differentiate under the integral, but instead put the derivative of the charge density in the integral, like in

$${\cal E}_x = - \frac{\partial \varphi}{\partial x} = - \... ...rtial {\underline x}} {\,\rm d}^3{\underline{\skew0\vec r}}$$

and similar for the $y$ and $z$ components. That you can do that may be verified by noting that differentiating ${\skew0\vec r}-{\underline{\skew0\vec r}}$ with respect to $x$ is within a minus sign the same as differentiating with respect to ${\underline x}$, and then you can use integration by parts to move the derivative to $\rho$.

Now consider the case that the charge distribution is restricted to a very small region around the origin, or equivalently, that the charge distribution is viewed from a very large distance. For simplicity, assume the case that the charge distribution is restricted to a small region around the origin. In that case, ${\underline{\skew0\vec r}}$ is small wherever there is charge; the integrand can therefore be approximated by a Taylor series in terms of ${\underline{\skew0\vec r}}$ to give:

$$\varphi = \frac{1}{4\pi\epsilon_0} \int_{{\rm all\ }{\unde... ...derline{\skew0\vec r}}) {\,\rm d}^3{\underline{\skew0\vec r}}$$

where (13.20) was used to evaluate the gradient of $1/\vert{\underline{\skew0\vec r}}-{\skew0\vec r}\vert$ with respect to ${\underline{\skew0\vec r}}$.

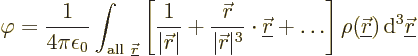
Since the fractions no longer involve ${\underline{\skew0\vec r}}$, they can be taken out of the integrals and so the potential simplifies to

$$\varphi = \frac{q}{4\pi\epsilon_0} \frac{1}{r} + \frac{1... ...erline{\skew0\vec r}}){\,\rm d}^3{\underline{\skew0\vec r}} %$$ (13.27)

The leading term shows that a distributed charge distribution will normally look like a point charge located at the origin when seen from a sufficient distance. However, if the net charge $q$ is zero, like happens for a neutral atom or molecule, it will look like an ideal dipole, the second term, when seen from a sufficient distance.

The expansion (13.27) is called a “multipole expansion.” It allows the effect of a complicated charge distribution to be described by a few simple terms, assuming that the distance from the charge distribution is sufficiently large that its small scale features can be ignored. If necessary, the accuracy of the expansion can be improved by using more terms in the Taylor series. Now recall from the previous section that one advantage of Maxwell’s equations over Coulomb’s law is that they allow you to describe the electric field at a point using purely local quantities, rather than having to consider the charges everywhere. But using a multipole expansion, you can simplify the effects of distant charge distributions. Then Coulomb’s law can become competitive with Maxwell’s equations, especially in cases where the charge distribution is restricted to a relatively limited fraction of the total space.

The previous subsection discussed how an ideal dipole could be created by decreasing the distance between two opposite charges with a compensating increase in their strength. The multipole expansion above shows that the same ideal dipole is obtained for a continuous charge distribution, provided that the net charge $q$ is zero.

The electric field of this ideal dipole can be found as minus the gradient of the potential. But caution is needed; the so-obtained electric field may not be sufficient for your needs. Consider the following ballpark estimates. Assume that the charge distribution has been contracted to a typical small size $\varepsilon$. Then the net positive and negative charges will have been increased by a corresponding factor $1/\varepsilon$. The electric field within the contracted charge distribution will then have a typical magnitude $1/\varepsilon\vert{\underline{\skew0\vec r}}-{\skew0\vec r}\vert^2$, and that means $1/\varepsilon^3$, since the typical size of the region is $\varepsilon$. Now a quantity of order $1/\varepsilon^3$ can integrate to a finite amount even if the volume of integration is small of order $\varepsilon^3$. In other words, there seems to be a possibility that the electric field may have a delta function hidden within the charge distribution when it is contracted to a point. And so it does. The correct delta function is derived in derivation {D.74} and shown in table 13.2. It is important in applications in quantum mechanics where you need some integral of the electric field; if you forget about the delta function, you will get the wrong result.

13.3.4 Solution of the Poisson equation

The previous subsections stumbled onto the solution of an important mathematical problem, the Poisson equation. The Poisson equation is

$$\nabla^2 \varphi = f$$ (13.28)

where $f$ is a given function and $\varphi$ is the unknown one to be found. The Laplacian $\nabla^2$ is also often found written as $\Delta$.

The reason that the previous subsection stumbled on to the solution of this equation is that the electric potential $\varphi$ satisfies it. In particular, minus the gradient of $\varphi$ gives the electric field; also, the divergence of the electric field gives according to Maxwell’s first equation the charge density $\rho$ divided by $\epsilon_0$. Put the two together and it says that $\nabla^2\varphi=-\rho/\epsilon_0$. So, identify the function $f$ in the Poisson equation with $-\rho/\epsilon_0$, and there you have the solution of the Poisson equation.

Because it is such an important problem, it is a good idea to write out the abstract mathematical solution without the “physical entourage” of (13.26):

$$\nabla^2\varphi=f \quad\Longrightarrow\quad \varphi({\sk... ...\skew0\vec r}) = - \frac{1}{4\pi \vert{\skew0\vec r}\vert} %$$ (13.29)

The function $G({\skew0\vec r}-{\underline{\skew0\vec r}})$ is called the Green’s function of the Laplacian. It is the solution for $\varphi$ if the function $f$ is a delta function at point ${\underline{\skew0\vec r}}$. The integral solution of the Poisson equation can therefore be understood as dividing function $f$ up into spikes $f({\underline{\skew0\vec r}}){\,\rm d}^3{\underline{\skew0\vec r}}$; for each of these spikes the contribution to $\varphi$ is given by corresponding Green's function.

It also follows that applying the Laplacian on the Green’s function produces the three-dimensional delta function,

$$\nabla^2 G({\skew0\vec r}) = \delta^3({\skew0\vec r}) \qqu... ...\skew0\vec r}) = - \frac{1}{4\pi \vert{\skew0\vec r}\vert} %$$ (13.30)

with $\vert{\skew0\vec r}\vert=r$ in spherical coordinates. That sometimes pops up in quantum mechanics, in particular in perturbation theory. You might object that the Green’s function is infinite at ${\skew0\vec r}=0$, so that its Laplacian is undefined there, rather than a delta function spike. And you would be perfectly right; just saying that the Laplacian of the Green’s function is the delta function is not really justified. However, if you slightly round the Green’s function near ${\skew0\vec r}=0$, say like $\varphi$ was rounded in figure 13.7, its Laplacian does exist everywhere. The Laplacian of this rounded Green’s function is a spike confined to the region of rounding, and it integrates to one. (You can see the latter from applying the divergence theorem on a sphere enclosing the region of rounding.) If you then contract the region of rounding to zero, this spike becomes a delta function in the limit of no rounding. Understood in this way, the Laplacian of the Green’s function is indeed a delta function.

The multipole expansion for a charge distribution can also be converted to purely mathematical terms:

$$\varphi = - \frac{1}{4\pi r} \int_{{\rm all\ }{\underline{... ...0\vec r}}){\,\rm d}^3{\underline{\skew0\vec r}} + \ldots %$$ (13.31)

(Of course, delta functions are infinite objects, and you might wonder at the mathematical rigor of the various arguments above. However, there are solid arguments based on “Green’s second integral identity” that avoid the infinities and produce the same final results.)

13.3.5 Currents

Streams of moving electric charges are called currents. The current strength $I$ through an electric wire is defined as the amount of charge flowing through a cross section per unit time. It equals the amount of charge $q'$ per unit length times its velocity $v$;

$$I \equiv q' v %$$ (13.32)

The current density $\vec\jmath$ is defined as the current per unit volume, and equals the charge density times the charge velocity. Integrating the current density over the cross section of a wire gives its current.

Figure 13.13: Magnetic field lines around an infinite straight electric wire.

As shown in figure 13.13, electric wires are encircled by magnetic field lines. The strength of this magnetic field may be computed from Maxwell’s fourth equation. To do so, take an arbitrary field line circle. The field strength is constant on the line by symmetry. So the integral of the field strength along the line is just $2{\pi}r{\cal B}$; the perimeter of the field line times its magnetic strength. Now the Stokes’ theorem of calculus says that this integral is equal to the curl of the magnetic field integrated over the interior of the field line circle. And Maxwell’s fourth equation says that that is $1/\epsilon_0c^2$ times the current density integrated over the circle. And the current density integrated over the circle is just the current through the wire. Put it all together to get

$$\mbox{magnetic field of an infinite straight wire:}\quad {\cal B}= \frac{I}{2\pi\epsilon_0c^2r} %$$ (13.33)

Figure 13.14: An electromagnet consisting of a single wire loop. The generated magnetic field lines are in blue.

An infinite straight wire is of course not a practical way to create a magnetic field. In a typical electromagnet, the wire is spooled around an iron bar. Figure 13.14 shows the field produced by a single wire loop, in vacuum. To find the fields produced by curved wires, use the so-called “Biot-Savart law” listed in table 13.2 and derived in {D.74}. You need it when you end up writing a book on quantum mechanics and have to plot the field.

Figure 13.15: A current dipole.

Of course, while figure 13.14 does not show it, you will also need a lead from your battery to the electromagnet and a second lead back to the other pole of the battery. These two leads form a two-dimensional “current dipole,” as shown in figure 13.15, and they produce a magnetic field too. However, the currents in the two leads are opposite; one coming from the battery and other returning to it, so the magnetic fields that they create are opposite. Therefore, if you strand the wires very closely together, their magnetic fields will cancel each other, and not mess up that of your electromagnet.

It may be noted that if you bring the wires close together, whatever is left of the field has circular field lines that touch at the dipole. In other words, a horizontal ideal current dipole produces the same field as a two-dimensional vertical ideal charge dipole. Similarly, the horizontal wire loop, if small enough, produces the same field lines as a three-dimensional vertical ideal charge dipole. (However, the delta functions are different, {D.74}.)

13.3.6 Principle of the electric motor

The previous section discussed how Maxwell’s third equation allows electric power generation using mechanical means. The converse is also possible; electric power allows mechanical power to be generated; that is the principle of the electric motor.

Figure 13.16: Electric motor using a single wire loop. The Lorentz forces (black vectors) exerted by the external magnetic field on the electric current carriers in the wire produce a net moment $M$ on the loop. The self-induced magnetic field of the wire and the corresponding radial forces are not shown.

It is possible because of the Lorentz force law, which says that a charge $q$ moving with velocity $\vec{v}$ in a magnetic field $\skew2\vec{\cal B}$ experiences a force pushing it sideways equal to

$$\vec F = q \vec v \times \skew2\vec{\cal B}$$

Consider the wire loop in an external magnetic field sketched in figure 13.16. The sideways forces on the current carriers in the wire produce a net moment $\vec{M}$ on the wire loop that allows it to perform useful work.

Figure 13.17: Variables for the computation of the moment on a wire loop in a magnetic field.

To be more precise, the forces caused by the component of the magnetic field normal to the wire loop are radial and produce no net force nor moment. However, the forces caused by the component of the magnetic field parallel to the loop produce forces normal to the plane of the loop that do generate a net moment. Using spherical coordinates aligned with the wire loop as in figure 13.17, the component of the magnetic field parallel to the loop equals ${\cal B}_{\rm {ext}}\sin\theta$. It causes a sideways force on each element $r{\rm d}\phi$ of the wire equal to

$${\rm d}F = \underbrace{q'r{\rm d}\phi}_{{\rm d}q} \und... ...a\sin\phi} _{\vec v\times\skew2\vec{\cal B}_{\rm parallel}}$$

where $q'$ is the net charge of current carriers per unit length and $v$ their velocity. The corresponding net force integrates to zero. However the moment does not; integrating

$${\rm d}M = \underbrace{r \sin\phi}_{\rm arm} \underbrace... ...\phi v {\cal B}_{\rm {ext}}\sin\theta\sin\phi} _{\rm force}$$

produces

$$M = \pi r^2 q' v {\cal B}_{\rm ext}\sin\theta$$

If the work $M{\rm d}\theta$ done by this moment is formulated as a change in energy of the loop in the magnetic field, that energy is

$$E_{\rm ext} = - \pi r^2 q' v {\cal B}_{\rm ext}\cos\theta$$

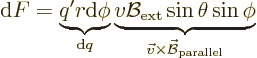
The magnetic dipole moment $\vec\mu$ is defined as the factor that only depends on the wire loop, independent of the magnetic field. In particular $\mu={\pi}r^2q'v$ and it is taken to be in the axial direction. So the moment and energy can be written more concisely as

$$\vec M = \vec\mu \times \skew2\vec{\cal B}_{\rm ext} \qquad E_{\rm ext} = - \vec\mu \cdot \skew2\vec{\cal B}_{\rm ext}$$

Yes, $\vec\mu$ also governs how the magnetic field looks at large distances; feel free to approximate the Biot-Savart integral for large distances to check.

A book on electromagnetics would typically identify $q'v$ with the current through the wire $I$ and ${\pi}r^2$ with the area of the loop, so that the magnetic dipole moment is just $IA$. This is then valid for a flat wire loop of any shape, not just a circular one.

But this is a book on quantum mechanics, and for electrons in orbits about nuclei, currents and areas are not very useful. In quantum mechanics the more meaningful quantity is angular momentum. So identify $2{\pi}rq'$ as the total electric charge going around in the wire loop, and multiply that with the ratio $m_{\rm {c}}/q_{\rm {c}}$ of mass of the current carrier to its charge to get the total mass going around. Then multiply with $rv$ to get the angular momentum $L$. In those terms, the magnetic dipole moment is

$$\vec\mu = \frac{q_{\rm c}}{2m_{\rm c}} \vec L %$$ (13.34)

Usually the current carrier is an electron, so $q_{\rm {c}}=-e$ and $m_{\rm {c}}=m_{\rm e}$.

These results apply to any arbitrary current distribution, not just a circular wire loop. Formulae are in table 13.2 and general derivations in {D.74}.