| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.11 Extension to three-dimensional solutions
Maybe you have some doubt whether you really can just multiply
one-dimensional eigenfunctions together, and add one-dimensional
energy values to get the three-dimensional ones. Would a book that
you find for free on the Internet lie? OK, let’s look at the
details then. First, the three-dimensional Hamiltonian, (really just
the kinetic energy operator), is the sum of the one-dimensional ones:
where the one-dimensional Hamiltonians are:
To check that any product 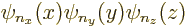 of
one-dimensional eigenfunctions is an eigenfunction of the combined
Hamiltonian
of
one-dimensional eigenfunctions is an eigenfunction of the combined
Hamiltonian  , note that the partial Hamiltonians only act on
their own eigenfunction, multiplying it by the corresponding
eigenvalue:
, note that the partial Hamiltonians only act on
their own eigenfunction, multiplying it by the corresponding
eigenvalue:
or
Therefore, by definition 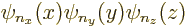 is
an eigenfunction of the three-dimensional Hamiltonian, with an
eigenvalue that is the sum of the three one-dimensional ones. But
there is still the question of completeness. Maybe the above
eigenfunctions are not complete, which would mean a need for
additional eigenfunctions that are not products of one-dimensional
ones.
is
an eigenfunction of the three-dimensional Hamiltonian, with an
eigenvalue that is the sum of the three one-dimensional ones. But
there is still the question of completeness. Maybe the above
eigenfunctions are not complete, which would mean a need for
additional eigenfunctions that are not products of one-dimensional
ones.
The one-dimensional eigenfunctions  are complete, see
[41, p. 141] and earlier exercises in this book. So,
you can write any wave function
are complete, see
[41, p. 141] and earlier exercises in this book. So,
you can write any wave function 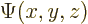 at given values of
at given values of  and
and  as a combination of
as a combination of
 -eigenfunctions:
-eigenfunctions:
but the coefficients 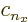 will be different for different values
of
will be different for different values
of  and
and  ; in other words they will be functions of
; in other words they will be functions of  and
and
 :
: 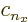

 . So, more precisely,
you have
. So, more precisely,
you have
But since the  -eigenfunctions are also complete, at any given value of
-eigenfunctions are also complete, at any given value of  , you can write each
, you can write each  as
a sum of
as
a sum of  -eigenfunctions:
-eigenfunctions:
where the coefficients 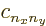 will be different for different
values of
will be different for different
values of  ,
, 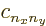

 . So,
more precisely,
. So,
more precisely,
But since the  -eigenfunctions are also complete, you can
write
-eigenfunctions are also complete, you can
write  as a sum of
as a sum of  -eigenfunctions:
-eigenfunctions:
Since the order of doing the summation does not make a difference,
So, any wave function 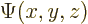 can be written as a sum of
products of one-dimensional eigenfunctions; these products are
complete.
can be written as a sum of
products of one-dimensional eigenfunctions; these products are
complete.
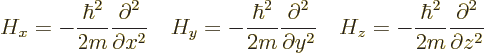
![]()
![]() ,
,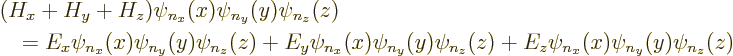
![]()
![]()
![]()
![]()
![]()
![]() -
-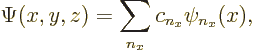
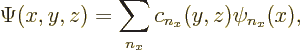
![]() -
-![]()
![]()
![]() -
-
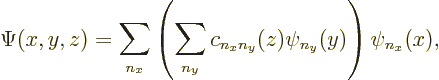
![]() -
-![]()
![]() -
-

![]()