| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.50 Spin degeneracy
To see that generally speaking the basic form of the Hamiltonian
produces energy degeneracy with respect to spin, but that it is not
important for using the Born-Oppenheimer approximation, consider the
example of three electrons.
Any three-electron energy eigenfunction 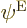 with
with
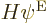

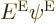 can be split into separate spatial functions
for the distinct combinations of electron spin values as
can be split into separate spatial functions
for the distinct combinations of electron spin values as
Since the assumed Hamiltonian 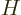 does not involve spin, each of the
eight spatial functions
does not involve spin, each of the
eight spatial functions  above will separately have
to be an eigenfunction of the Hamiltonian with eigenvalue
above will separately have
to be an eigenfunction of the Hamiltonian with eigenvalue  if
nonzero. In addition, since the first four functions have an odd
number of spin up states and the second four an even number, the
antisymmetry requirements apply only within the two sets, not between
them. The exchanges only affect the order of the spin states, not
their number. So the two sets satisfy the antisymmetry requirements
individually.
if
nonzero. In addition, since the first four functions have an odd
number of spin up states and the second four an even number, the
antisymmetry requirements apply only within the two sets, not between
them. The exchanges only affect the order of the spin states, not
their number. So the two sets satisfy the antisymmetry requirements
individually.
It is now seen that given a solution for the first four wave
functions, there is an equally good solution for the second four wave
functions that is obtained by inverting all the spins. Since the
spins are not in the Hamiltonian, inverting the spins does not change
the energy. They have the same energy, but are different because they
have different spins.
However, they are orthogonal because their spins are, and the spatial
operations in the derivation of the Born-Oppenheimer approximation in
the next note do not change that fact. So they turn out to lead to
nuclear wave functions that do not affect each other. More precisely,
the inner products appearing in the coefficients 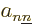 are zero
because the spins are orthogonal.
are zero
because the spins are orthogonal.
![]()
![]()
![]()
![]()
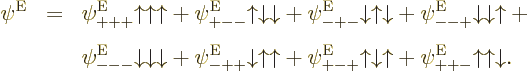
![]()
![]()
![]()
![]()