| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.51 Born-Oppenheimer nuclear motion
This note gives a derivation of the Born-Oppenheimer Hamiltonian
eigenvalue problems (9.14) for the wave functions of the
nuclei.
First consider an exact eigenfunction  of the complete system,
including both the electrons and the nuclei fully. Can it be related
somehow to the simpler electron eigenfunctions
of the complete system,
including both the electrons and the nuclei fully. Can it be related
somehow to the simpler electron eigenfunctions
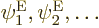 that ignored nuclear kinetic energy? Yes
it can. For any given set of nuclear coordinates, the electron
eigenfunctions are complete; they are the eigenfunctions of an
Hermitian electron Hamiltonian. And that means that you can for any
given set of nuclear coordinates write the exact wave function as
that ignored nuclear kinetic energy? Yes
it can. For any given set of nuclear coordinates, the electron
eigenfunctions are complete; they are the eigenfunctions of an
Hermitian electron Hamiltonian. And that means that you can for any
given set of nuclear coordinates write the exact wave function as
You can do this for any set of nuclear coordinates that you like, but
the coefficients  will be different for different sets of
nuclear coordinates. That is just another way of saying that the
will be different for different sets of
nuclear coordinates. That is just another way of saying that the
 are functions of the nuclear coordinates.
are functions of the nuclear coordinates.
So, to be really precise, the wave function of  electrons and
electrons and 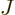 nuclei can be written as:
nuclei can be written as:
where superscripts n indicate nuclear coordinates. (The nuclear spins
are really irrelevant, but it cannot hurt to keep them in.)
Consider what this means physically. By construction, the square
electron eigenfunctions 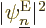 give the probability of
finding the electrons assuming that they are in eigenstate
give the probability of
finding the electrons assuming that they are in eigenstate 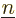 and that the nuclei
are at the positions listed in the final arguments of the electron
eigenfunction. But then the probability that the nuclei are
actually at those positions, and that the electrons are actually in
eigenstate
and that the nuclei
are at the positions listed in the final arguments of the electron
eigenfunction. But then the probability that the nuclei are
actually at those positions, and that the electrons are actually in
eigenstate 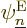 , will have to be
, will have to be 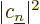 .
After all, the full wave function
.
After all, the full wave function  must describe the probability
for the entire system to actually be in a specific state. That
means that
must describe the probability
for the entire system to actually be in a specific state. That
means that  must be the nuclear wave function
must be the nuclear wave function 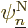 for
when the electrons are in energy eigenstate
for
when the electrons are in energy eigenstate 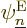 . So
from now on, just call it
. So
from now on, just call it 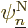 instead of
instead of  . The
full wave function is then
. The
full wave function is then
 |
(D.31) |
In the unsteady case, the  , hence the
, hence the
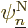 , will also be functions of time. The
, will also be functions of time. The
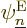 will remain time independent as long as no explicitly
time-dependent terms are added. The derivation then goes exactly the
same way as the time-independent Schrödinger equation (Hamiltonian
eigenvalue problem) derived below, with
will remain time independent as long as no explicitly
time-dependent terms are added. The derivation then goes exactly the
same way as the time-independent Schrödinger equation (Hamiltonian
eigenvalue problem) derived below, with
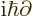

 replacing
replacing  .
.
So far, no approximations have been made; the only thing that has been
done is to define the nuclear wave functions 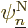 . But
the objective is still to derive the claimed equation
(9.14) for them. To do so plug the expression
. But
the objective is still to derive the claimed equation
(9.14) for them. To do so plug the expression 

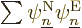 into the exact Hamiltonian eigenvalue
problem:
into the exact Hamiltonian eigenvalue
problem:
Note first that the eigenfunctions can be taken to be real since the
Hamiltonian is real. If the eigenfunctions were complex, then their
real and imaginary parts separately would be eigenfunctions, and both
of these are real. This argument applies to both the electron
eigenfunctions separately as well as to the full eigenfunction. The
trick is now to take an inner product of the equation above with a
chosen electron eigenfunction 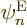 . More precisely,
multiply the entire equation by
. More precisely,
multiply the entire equation by 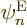 , and integrate/sum
over the electron coordinates and spins only, keeping the nuclear
positions and spins at fixed values.
, and integrate/sum
over the electron coordinates and spins only, keeping the nuclear
positions and spins at fixed values.
What do you get? Consider the terms in reverse order, from right to
left. In the right hand side, the electron-coordinate inner product
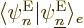 is zero unless
is zero unless 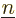

 , and then it is one, since the electron wave functions are
orthonormal for given nuclear coordinates. So all we have left in the
right-hand side is
, and then it is one, since the electron wave functions are
orthonormal for given nuclear coordinates. So all we have left in the
right-hand side is 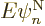 , Check,
, Check, 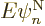 is the
correct right hand side in the nuclear-wave-function Hamiltonian
eigenvalue problem (9.14).
is the
correct right hand side in the nuclear-wave-function Hamiltonian
eigenvalue problem (9.14).
Turning to the latter four terms in the left-hand side, remember that
by definition the electron eigenfunctions satisfy
and if you then take an inner product of
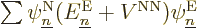 with
with 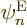 ,
it is just like the earlier term, and you get
,
it is just like the earlier term, and you get
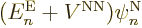 . Check, that are two of the terms in
the left-hand side of (9.14) that you need.
. Check, that are two of the terms in
the left-hand side of (9.14) that you need.
That leaves only the nuclear kinetic term, and that one is a bit
tricky. Recalling the definition (9.5) of the kinetic
energy operator 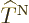 in terms of the nuclear coordinate Laplacians,
you have
in terms of the nuclear coordinate Laplacians,
you have
Remember that not just the nuclear wave functions, but also the
electron wave functions depend on the nuclear coordinates. So, if you
differentiate out the product, you get
Now if you take the inner product with electron eigenfunction
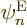 , the first term in the brackets gives you what you
need, the expression for the kinetic energy of the nuclei. But you do
not want the other two terms; these terms have the nuclear kinetic
energy differentiations at least in part on the electron wave
function instead of on the nuclear wave function.
, the first term in the brackets gives you what you
need, the expression for the kinetic energy of the nuclei. But you do
not want the other two terms; these terms have the nuclear kinetic
energy differentiations at least in part on the electron wave
function instead of on the nuclear wave function.
Well, whether you like it or not, the exact equation is, collecting
all terms and rearranging,
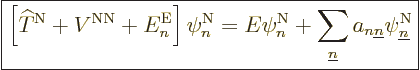 |
(D.32) |
where
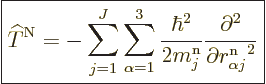 |
(D.33) |
 |
(D.34) |
The first thing to note is the final sum in (D.32). Unless
you can talk away this sum as negligible, (9.14) is not
valid. The off-diagonal
coefficients, the 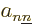 for
for 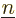
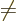
 , are particularly bad news, because they
produce interactions between the different potential energy surfaces,
shifting energy from one value of
, are particularly bad news, because they
produce interactions between the different potential energy surfaces,
shifting energy from one value of  to another. These off-diagonal
terms are called “vibronic coupling terms.” (The word is a contraction of
to another. These off-diagonal
terms are called “vibronic coupling terms.” (The word is a contraction of
vibration” and “electronic,
if you are
wondering.)
Let’s have a closer look at (D.33) and
(D.34) to see how big the various terms really are. At
first appearance it might seem that both the nuclear kinetic energy
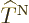 and the coefficients
and the coefficients 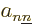 can be ignored, since both are
inversely proportional to the nuclear masses, hence apparently
thousands of times smaller than the electronic kinetic energy included
in
can be ignored, since both are
inversely proportional to the nuclear masses, hence apparently
thousands of times smaller than the electronic kinetic energy included
in 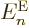 . But do not go too quick here. First ballpark the
typical derivative,
. But do not go too quick here. First ballpark the
typical derivative, 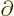

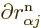 when
applied to the nuclear wave function. You can estimate such a
derivative as 1/
when
applied to the nuclear wave function. You can estimate such a
derivative as 1/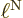 , where
, where 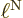 is the typical length
over which there are significant changes in a nuclear wave function
is the typical length
over which there are significant changes in a nuclear wave function
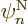 . Well, there are significant changes in nuclear
wave functions if you go from the middle of a nucleus to its outside,
and that is a very small distance compared to the typical size of the
electron blob
. Well, there are significant changes in nuclear
wave functions if you go from the middle of a nucleus to its outside,
and that is a very small distance compared to the typical size of the
electron blob  . It means that the distance
. It means that the distance 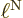 is small. So the relative importance of the nuclear kinetic energy
increases by a factor
is small. So the relative importance of the nuclear kinetic energy
increases by a factor  relative to the electron
kinetic energy, compensating quite a lot for the much higher nuclear
mass. So keeping the nuclear kinetic energy is definitely a good
idea.
relative to the electron
kinetic energy, compensating quite a lot for the much higher nuclear
mass. So keeping the nuclear kinetic energy is definitely a good
idea.
How about the coefficients 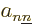 ? Well, normally
the electron eigenfunctions only change appreciable when you vary the
nuclear positions over a length comparable to the electron blob scale
? Well, normally
the electron eigenfunctions only change appreciable when you vary the
nuclear positions over a length comparable to the electron blob scale
 . Think back of the example of the hydrogen molecule.
The ground state separation between the nuclei was found as 0.87Å.
But you would not see a dramatic change in electron wave functions if
you made it a few percent more or less. To see a dramatic change, you
would have to make the nuclear distance 1.5Å, for example. So the
derivatives
. Think back of the example of the hydrogen molecule.
The ground state separation between the nuclei was found as 0.87Å.
But you would not see a dramatic change in electron wave functions if
you made it a few percent more or less. To see a dramatic change, you
would have to make the nuclear distance 1.5Å, for example. So the
derivatives 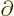

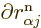 applied to the
electron wave functions are normally not by far as large as those
applied to the nuclear wave functions, hence the
applied to the
electron wave functions are normally not by far as large as those
applied to the nuclear wave functions, hence the 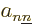 terms are
relatively small compared to the nuclear kinetic energy, and ignoring
them is usually justified. So the final conclusion is that equation
(9.14) is usually justified.
terms are
relatively small compared to the nuclear kinetic energy, and ignoring
them is usually justified. So the final conclusion is that equation
(9.14) is usually justified.
But there are exceptions. If different energy levels get close
together, the electron wave functions become very sensitive to small
effects, including small changes in the nuclear positions. When the
wave functions have become sensitive enough that they vary
significantly under nuclear position changes comparable in size to the
nuclear wave function blobs, you can no longer ignore the 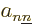 terms and (9.14) becomes invalid.
terms and (9.14) becomes invalid.
You can be a bit more precise about that claim with a few tricks.
Consider the factors
appearing in the 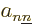 , (D.34). First of all,
these factors are zero when
, (D.34). First of all,
these factors are zero when 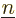

 . The reason is that
because of orthonormality,
. The reason is that
because of orthonormality, 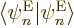
 1, and taking the
1, and taking the 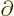

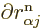 derivative
of that, noting that the eigenfunctions are real, you see that the
factor is zero.
derivative
of that, noting that the eigenfunctions are real, you see that the
factor is zero.
For 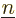
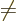
 , the following trick works:
, the following trick works:
The first equality is just a matter of the definition of the electron
eigenfunctions and taking the second 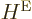 to the other side, which
you can do since it is Hermitian. The second equality is a matter of
looking up the Hamiltonian in chapter 9.2.1 and then working
out the commutator in the leftmost inner product. (
to the other side, which
you can do since it is Hermitian. The second equality is a matter of
looking up the Hamiltonian in chapter 9.2.1 and then working
out the commutator in the leftmost inner product. (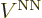 does not
commute with the derivative, but you can use orthogonality on the
cleaned up expression.) The bottom line is that the final inner
product is finite, with no reason for it to become zero when energy
levels approach. So, looking at the second equality, the first term
in
does not
commute with the derivative, but you can use orthogonality on the
cleaned up expression.) The bottom line is that the final inner
product is finite, with no reason for it to become zero when energy
levels approach. So, looking at the second equality, the first term
in 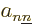 , (D.34), blows up like
1
, (D.34), blows up like
1
 when those energy levels become equal.
when those energy levels become equal.
As far as the final term in 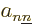 is concerned, like the second
term, you would expect it to become important when the scale of
nontrivial changes in electron wave functions with nuclear positions
becomes comparable to the size of the nuclear wave functions. You can
be a little bit more precise by taking one more derivative of the
inner product expression derived above,
is concerned, like the second
term, you would expect it to become important when the scale of
nontrivial changes in electron wave functions with nuclear positions
becomes comparable to the size of the nuclear wave functions. You can
be a little bit more precise by taking one more derivative of the
inner product expression derived above,
The first term should not be large: while the left hand side of the
inner product has a large component along 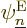 , the
other side has zero component and vice-versa. The final term should
be of order 1/
, the
other side has zero component and vice-versa. The final term should
be of order 1/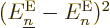 , as you can see if you first
change the origin of the integration variable in the inner product to
be at the nuclear position, to avoid having to differentiate the
potential derivative. So you conclude that the second term of
coefficient
, as you can see if you first
change the origin of the integration variable in the inner product to
be at the nuclear position, to avoid having to differentiate the
potential derivative. So you conclude that the second term of
coefficient 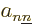 is of order 1/
is of order 1/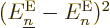 . In
view of the fact that this term has one less derivative on the nuclear
wave function, that is just enough to allow it to become significant
at about the same time that the first term does.
. In
view of the fact that this term has one less derivative on the nuclear
wave function, that is just enough to allow it to become significant
at about the same time that the first term does.
The diagonal part of matrix 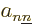 , i.e. the
, i.e. the  terms,
is somewhat interesting since it produces a change in effective energy
without involving interactions with the other potential energy
surfaces, i.e. without interaction with the
terms,
is somewhat interesting since it produces a change in effective energy
without involving interactions with the other potential energy
surfaces, i.e. without interaction with the 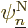 for
for 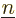
 . The diagonal part is called the “Born-Oppenheimer diagonal correction.” Since as noted above,
the first term in the expression (D.34) for the
. The diagonal part is called the “Born-Oppenheimer diagonal correction.” Since as noted above,
the first term in the expression (D.34) for the 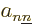 does not have a diagonal part, the diagonal correction is given by the
second term.
does not have a diagonal part, the diagonal correction is given by the
second term.
Note that in a transient case that starts out as a single nuclear wave
function 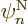 , the diagonal term
, the diagonal term  multiplies the
predominant nuclear wave function
multiplies the
predominant nuclear wave function 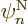 , while the
off-diagonal terms only multiply the small other nuclear wave
functions. So despite not involving any derivative of the nuclear
wave function, the diagonal term will initially be the main correction
to the Born-Oppenheimer approximation. It will remain important at
later times.
, while the
off-diagonal terms only multiply the small other nuclear wave
functions. So despite not involving any derivative of the nuclear
wave function, the diagonal term will initially be the main correction
to the Born-Oppenheimer approximation. It will remain important at
later times.
![]()
![]()

![]()
![]()
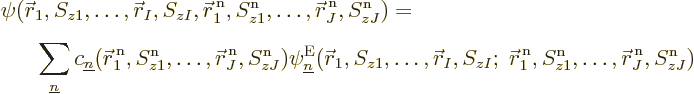
![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]()
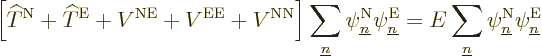
![]() .
.![]() ,
,![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
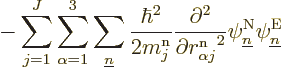
![\begin{displaymath}
- \sum_{j=1}^J\sum_{\alpha=1}^3\sum_{\underline n}
\left[
...
...e n}}{\partial r^{\rm n}_{\alpha j}\rule{0pt}{8pt}^2}
\right]
\end{displaymath}](img6965.gif)
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]() .
.![]() .
.![]()
![]()
![]() ?
?![]() .
.![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]() ,
,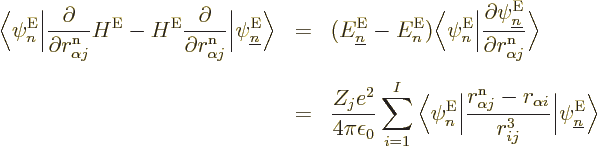
![]()

![]() ,
,![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]() ,
,