| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.8 Completeness of Fourier modes
The purpose of this note is to show completeness of the
Fourier modes
for describing functions that are periodic of period  . It
is to be shown that
. It
is to be shown that all
these functions can be written
as combinations of the Fourier modes above. Assume that  is any
reasonable smooth function that repeats itself after a distance
is any
reasonable smooth function that repeats itself after a distance
 , so that
, so that 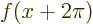

 . Then you can
always write it in the form
. Then you can
always write it in the form
or
for short. Such a representation of a periodic function is called a
“Fourier series.” The coefficients 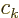 are called “Fourier coefficients.” The factors 1
are called “Fourier coefficients.” The factors 1
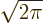 can be
absorbed in the definition of the Fourier coefficients, if you want.
can be
absorbed in the definition of the Fourier coefficients, if you want.
Because of the Euler formula, the set of exponential Fourier modes
above is completely equivalent to the set of real Fourier modes
so that  -periodic functions may just as well be written as
-periodic functions may just as well be written as
The extension to functions that are periodic of some other period than
 is a trivial matter of rescaling
is a trivial matter of rescaling  . For a period
. For a period
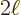 , with
, with  any half period, the exponential Fourier
modes take the more general form
any half period, the exponential Fourier
modes take the more general form
and similarly the real version of them becomes
See [41, p. 141] for detailed formulae.
Often, the functions of interest are not periodic, but are required to
be zero at the ends of the interval on which they are defined. Those
functions can be handled too, by extending them to a periodic
function. For example, if the functions  relevant to a problem
are defined only for 0
relevant to a problem
are defined only for 0 


 and must satisfy
and must satisfy 

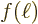
 0, then extend them to the range
0, then extend them to the range 



 0 by setting
0 by setting 

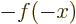 and take the range
and take the range





 to be the period of a
to be the period of a
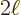 -periodic function. It may be noted that for such a
function, the cosines disappear in the real Fourier series
representation, leaving only the sines. Similar extensions can be
used for functions that satisfy symmetry or zero-derivative boundary
conditions at the ends of the interval on which they are defined. See
again [41, p. 141] for more detailed formulae.
-periodic function. It may be noted that for such a
function, the cosines disappear in the real Fourier series
representation, leaving only the sines. Similar extensions can be
used for functions that satisfy symmetry or zero-derivative boundary
conditions at the ends of the interval on which they are defined. See
again [41, p. 141] for more detailed formulae.
If the half period  becomes infinite, the spacing between the
discrete
becomes infinite, the spacing between the
discrete  values becomes zero and the sum over discrete
values becomes zero and the sum over discrete  values
turns into an integral over continuous
values
turns into an integral over continuous  values. This is exactly
what happens in quantum mechanics for the eigenfunctions of linear
momentum. The representation is now no longer called a Fourier
series, but a “Fourier integral.” And the Fourier coefficients
values. This is exactly
what happens in quantum mechanics for the eigenfunctions of linear
momentum. The representation is now no longer called a Fourier
series, but a “Fourier integral.” And the Fourier coefficients 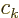 are now
called the “Fourier transform”
are now
called the “Fourier transform” 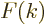 . The completeness of the
eigenfunctions is now called Fourier’s integral theorem or
inversion theorem. See [41, pp. 190-191] for more.
. The completeness of the
eigenfunctions is now called Fourier’s integral theorem or
inversion theorem. See [41, pp. 190-191] for more.
The basic completeness proof is a rather messy mathematical
derivation, so read the rest of this note at your own risk. The fact
that the Fourier modes are orthogonal and normalized was the subject
of various exercises in chapter 2.6 and will be taken for
granted here. See the solution manual for the details. What this
note wants to show is that any arbitrary periodic function  of period
of period  that has continuous first and second order
derivatives can be written as
that has continuous first and second order
derivatives can be written as
in other words, as a combination of the set of Fourier modes.
First an expression for the values of the Fourier coefficients 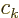 is needed. It can be obtained from taking the inner product
is needed. It can be obtained from taking the inner product
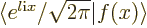 between a
generic eigenfunction
between a
generic eigenfunction 

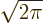 and the
representation for function
and the
representation for function  above. Noting that all the inner
products with the exponentials representing
above. Noting that all the inner
products with the exponentials representing  will be zero except
the one for which
will be zero except
the one for which 

 , if the Fourier representation
is indeed correct, the coefficients need to have the values
, if the Fourier representation
is indeed correct, the coefficients need to have the values
a requirement that was already noted by Fourier. Note that  and
and
 are just names for the eigenfunction number and the integration
variable that you can change at will. Therefore, to avoid name
conflicts later, the expression will be renotated as
are just names for the eigenfunction number and the integration
variable that you can change at will. Therefore, to avoid name
conflicts later, the expression will be renotated as
Now the question is: suppose you compute the Fourier coefficients
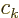 from this expression, and use them to sum many terms of the
infinite sum for
from this expression, and use them to sum many terms of the
infinite sum for  , say from some very large negative value
, say from some very large negative value

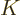 for
for  to the corresponding large positive value
to the corresponding large positive value 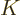 ;
in that case, is the result you get, call it
;
in that case, is the result you get, call it 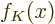 ,
,
a valid approximation to the true function  ? More
specifically, if you sum more and more terms (make
? More
specifically, if you sum more and more terms (make 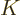 bigger and
bigger), does
bigger and
bigger), does 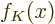 reproduce the true value of
reproduce the true value of  to any
arbitrary accuracy that you may want? If it does, then the
eigenfunctions are capable of reproducing
to any
arbitrary accuracy that you may want? If it does, then the
eigenfunctions are capable of reproducing  . If the
eigenfunctions are not complete, a definite difference between
. If the
eigenfunctions are not complete, a definite difference between
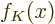 and
and  will persist however large you make
will persist however large you make 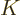 . In
mathematical terms, the question is whether
. In
mathematical terms, the question is whether 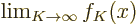

 .
.
To find out, the trick is to substitute the integral for the
coefficients 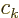 into the sum and then reverse the order of
integration and summation to get:
into the sum and then reverse the order of
integration and summation to get:
The sum in the square brackets can be evaluated, because it is a
geometric series with starting value 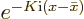 and ratio
of terms
and ratio
of terms 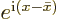 . Using the formula from [41, item 21.4], multiplying top and bottom with
. Using the formula from [41, item 21.4], multiplying top and bottom with
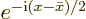 , and cleaning up with, what else, the
Euler formula, the sum is found to equal
, and cleaning up with, what else, the
Euler formula, the sum is found to equal
This expression is called the Dirichlet kernel
. You
now have
The second trick is to split the function 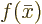 being
integrated into the two parts
being
integrated into the two parts  and
and  . The
sum of the parts is obviously still
. The
sum of the parts is obviously still 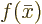 , but the first
part has the advantage that it is constant during the integration over
, but the first
part has the advantage that it is constant during the integration over
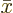 and can be taken out, and the second part has the advantage
that it becomes zero at
and can be taken out, and the second part has the advantage
that it becomes zero at 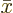

 . You get
. You get
Now if you backtrack what happens in the trivial case that  is
just a constant, you find that
is
just a constant, you find that 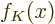 is exactly equal to
is exactly equal to  in
that case, while the second integral above is zero. That makes the
first integral above equal to one. Returning to the case of general
in
that case, while the second integral above is zero. That makes the
first integral above equal to one. Returning to the case of general
 , since the first integral above is still one, it makes
the first term in the right hand side equal to the desired
, since the first integral above is still one, it makes
the first term in the right hand side equal to the desired
 , and the second integral is then the error in
, and the second integral is then the error in
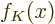 .
.
To manipulate this error and show that it is indeed small for large
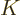 , it is convenient to rename the
, it is convenient to rename the 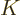 -independent part
of the integrand to
-independent part
of the integrand to
Using l’Hôpital's rule twice, it is seen that since by
assumption  has a continuous second derivative,
has a continuous second derivative,  has a
continuous first derivative. So you can use one integration by parts
to get
has a
continuous first derivative. So you can use one integration by parts
to get
And since the integrand of the final integral is continuous, it is
bounded. That makes the error inversely proportional to
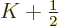 , implying that it does indeed become arbitrarily
small for large
, implying that it does indeed become arbitrarily
small for large 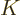 . Completeness has been proved.
. Completeness has been proved.
It may be noted that under the stated conditions, the convergence is
uniform; there is a guaranteed minimum rate of convergence regardless
of the value of  . This can be verified from Taylor series
with remainder. Also, the more continuous derivatives the
. This can be verified from Taylor series
with remainder. Also, the more continuous derivatives the
 -periodic function
-periodic function  has, the faster the rate of
convergence, and the smaller the number
has, the faster the rate of
convergence, and the smaller the number 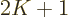 of terms that you need
to sum to get good accuracy is likely to be. For example, if
of terms that you need
to sum to get good accuracy is likely to be. For example, if  has three continuous derivatives, you can do another integration by
parts to show that the convergence is proportional to
1
has three continuous derivatives, you can do another integration by
parts to show that the convergence is proportional to
1
 rather than just 1/
rather than just 1/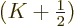 . But
watch the end points: if a derivative has different values at the
start and end of the period, then that derivative is not continuous,
it has a jump at the ends. (Such jumps can be incorporated in the
analysis, however, and have less effect than it may seem. You get a
better practical estimate of the convergence rate by directly looking
at the integral for the Fourier coefficients.)
. But
watch the end points: if a derivative has different values at the
start and end of the period, then that derivative is not continuous,
it has a jump at the ends. (Such jumps can be incorporated in the
analysis, however, and have less effect than it may seem. You get a
better practical estimate of the convergence rate by directly looking
at the integral for the Fourier coefficients.)
The condition for  to have a continuous second derivative can be
relaxed with more work. If you are familiar with the Lebesgue form of
integration, it is fairly easy to extend the result above to show that
it suffices that the absolute integral of
to have a continuous second derivative can be
relaxed with more work. If you are familiar with the Lebesgue form of
integration, it is fairly easy to extend the result above to show that
it suffices that the absolute integral of 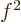 exists, something that
will be true in quantum mechanics applications.
exists, something that
will be true in quantum mechanics applications.
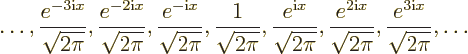
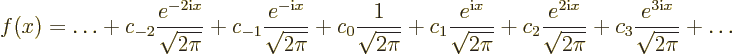
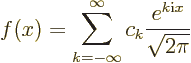
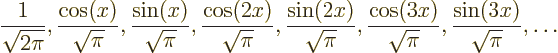
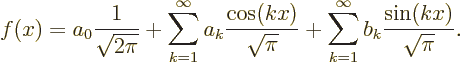
![]()
![]() .
.![]() ,
,![]()

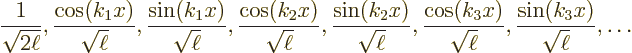
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
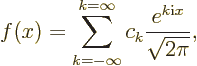
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
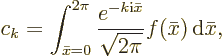
![]()
![]() ,
,![]()
![]()
![]()
![]() ;
;![]() ,
,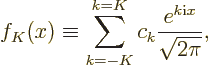
![]()
![\begin{displaymath}
f_K(x) = \frac{1}{2\pi} \int_{\bar x=0}^{2\pi} f(\bar x)
\...
...m_{k=-K}^{k=K} e^{k{\rm i}(x-\bar x)}\right]
{\,\rm d}\bar x.
\end{displaymath}](img5954.gif)
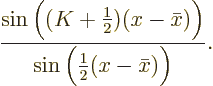
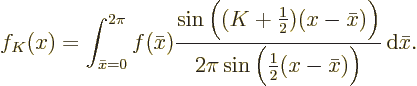
![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]()
![]() .
.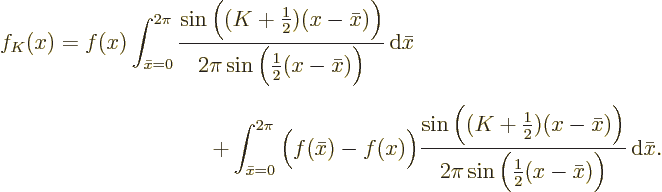
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() -
-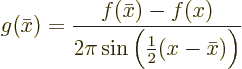
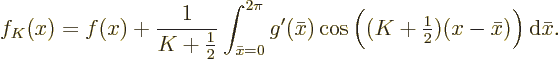
![]() .
.![]() -
-![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()