| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.9 Momentum operators are Hermitian
To check that the linear momentum operators are Hermitian, assume that
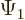 and
and 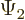 are any two proper, reasonably behaved, wave
functions. By definition:
are any two proper, reasonably behaved, wave
functions. By definition:
Here the subscript  indicates differentiation with respect to
indicates differentiation with respect to
 . This can be rewritten as
as can be checked by simply differentiating out the product in the
first term.
. This can be rewritten as
as can be checked by simply differentiating out the product in the
first term.
Now the first term in the integral can be integrated with respect to
 and is then seen to produce zero. The reason is that
and is then seen to produce zero. The reason is that 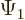 and
and
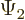 must become zero at large distances, otherwise their square
integral cannot be zero. That leaves only the second term. And that
equals
must become zero at large distances, otherwise their square
integral cannot be zero. That leaves only the second term. And that
equals
(Recall that the complex conjugate of  is
is 
 , hence the
minus sign.)
, hence the
minus sign.)
For the mathematically picky, it is maybe a good idea to examine the
claim that the first term in the integral in (1) integrates to zero a
bit more closely. The integral is definitely zero if the system is
not in infinite space, but in a periodic box. The reason is that in
that case the lower and upper limits of integration are equal and drop
out against each other. To be rigorous in infinite space, you will at
first need to limit the region of integration to a distance no more
than some large number  away from the origin. (It will be assumed
that the initial inner product is well defined, in the sense that the
integral has a finite limit in the limit
away from the origin. (It will be assumed
that the initial inner product is well defined, in the sense that the
integral has a finite limit in the limit 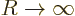 . In that
case, the integral can be approximated to arbitrary accuracy by just
taking
. In that
case, the integral can be approximated to arbitrary accuracy by just
taking  large enough.) Using the divergence theorem, the first
integral is
large enough.) Using the divergence theorem, the first
integral is
where 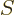 is the surface of the sphere
is the surface of the sphere 

 and
and 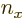 the
the
 -component of the unit vector
-component of the unit vector 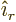 normal to the surface. Now
since the absolute square integrals of the wave functions are finite,
for large enough
normal to the surface. Now
since the absolute square integrals of the wave functions are finite,
for large enough  their square integrals outside
their square integrals outside  become
arbitrarily small. The Cauchy Schwartz inequality then says that the
above integral integrated with respect to
become
arbitrarily small. The Cauchy Schwartz inequality then says that the
above integral integrated with respect to  must become vanishingly
small. And that is not possible unless the integral itself becomes
vanishingly small at almost all locations. So you can define a
sequence for
must become vanishingly
small. And that is not possible unless the integral itself becomes
vanishingly small at almost all locations. So you can define a
sequence for  where the inner product with the linear momentum
swapped over approaches the original inner product. In particular,
the two inner products are equal to the degree that they are well
defined in the first place.
where the inner product with the linear momentum
swapped over approaches the original inner product. In particular,
the two inner products are equal to the degree that they are well
defined in the first place.
![]()
![]()

![$\parbox{400pt}{\hspace{11pt}\hfill$\displaystyle
\int_{x=-\infty}^\infty\int_{...
...* \frac{\hbar}{{\rm i}} \Psi_2
\right] {\,\rm d}x{\rm d}y{\rm d}z
$\hfill(1)}$](img5971.gif)
![]()
![]()
![]()
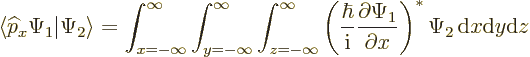
![]()
![]() .
.![]()
