|
|
|
|
|
Next: A.9 Wave function symmetries |
|
This addendum discusses why in at least the simplest cases a ground state wave function can be assumed to be real, positive, and unique (i.e. nondegenerate). It is assumed that the potential is a real function of position. That is true for the hydrogen molecular ion. It is also true for a single hydrogen atom and most other simple systems, at least in the nonrelativistic approximations normally used in this book.
It should first be noted that if potentials are allowed that are positive infinity in a finite region, nonunique ground states that cannot be taken positive may in fact possible. Such a potential can provide an impenetrable boundary, completely separating one region of space from another. In that case the ground state wave functions at the two sides of the boundary become decoupled, allowing for indeterminacy in the combined ground state. Such artificial cases are not covered here. But you can readily find examples in lots of books on quantum mechanics, especially in one dimension. Here it will be assumed that the potentials stay away from positive infinity. For practical purposes, it may also be noted that if the potential becomes positive infinity at just a few points, it is usually not a problem unless the approach to singularity is very steep.
There is however a much more important restriction to the conclusions in this note: ground states may not be positive if you go to many-particle systems. That is discussed further in the final paragraphs of this addendum.
First consider why the ground state, and any other energy eigenstate,
can be assumed to be real without loss of generality. Suppose that
you had a complex eigenfunction ![]()
![]()
![]()
![]() .
.
Next consider why the ground state can be taken to be positive,
assuming, for now, that it is unique. What characterizes the ground
state ![]()
![]()
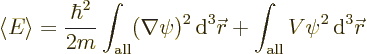
Finally, it needs to be shown that the ground state is indeed unique as assumed above. That is really messy, so it has been banned to derivation {D.22}. It is based on the same idea that the absolute value of a ground state is a ground state too.
Regrettably the arguments above stop working for more than two
electrons. To really understand the reason, you will first need to
read chapter 5.6 on multiple-particle systems. But in a
nutshell, the wave function for systems with multiple electrons must
satisfy additional requirements, called the
antisymmetrization
requirements. These
requirements normally turn ![]()
spin.
That allows the hydrogen
molecule, with two electrons, still to be covered.
The same problem occurs for atomic nuclei that contain multiple protons and/or neutrons. (For atomic nuclei, the potentials also tend to be far more complicated than assumed here. But that is another matter.) In general, particles for which antisymmetrization requirements apply are called fermions.
There is however a different class of particles called
”bosons.” For those, the wave function has to satisfy
symmetrization
requirements. Symmetrization
requirements are still OK if you replace ![]()
![]() .
.