A.7 Ac­cu­racy of the vari­a­tional method

This note has a closer look at the ac­cu­racy of the vari­a­tional method.

Any ap­prox­i­mate ground state wave func­tion $\psi$ may al­ways be writ­ten as a com­bi­na­tion of all the en­ergy eigen­func­tions $\psi_1$, $\psi_2$, ...:

$$\psi = c_1 \psi_1 + \delta_2 \psi_2 + \delta_3 \psi_3 + \ldots$$

where $c_1$ and the $\delta_i$ for $i$ $\vphantom0\raisebox{1.5pt}{$=$}$ 2, 3, ...are nu­mer­i­cal co­ef­fi­cients. But if the ap­prox­i­ma­tion is any good at all, the co­ef­fi­cient $c_1$ of the cor­rect ground state $\psi_1$ must be close to one, while the co­ef­fi­cients $\delta_i$ of the higher en­ergy states must be small.

The wave func­tion pol­lu­tion with higher en­ergy states can be re­lated to the er­ror in en­ergy, call it $\varepsilon$, us­ing a few sim­ple ma­nip­u­la­tions. First the con­di­tion that $\psi$ is nor­mal­ized, $\langle\psi\vert\psi\rangle$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1, works out to be

$$1 = \langle c_1\psi_1 +\delta_2\psi_2+\ldots \vert c_1\psi... ...si_2+\ldots\rangle = c_1^2 + \delta_2^2 + \delta_3^2 + \ldots$$

since the eigen­func­tions $\psi_1,\psi_2,\ldots$ are or­tho­nor­mal. Sim­i­larly, the ex­pec­ta­tion en­ergy $\langle{E}\rangle$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\langle\psi\vert H\psi\rangle$ of the ap­prox­i­mate so­lu­tion works out to be

$$\left\langle{E}\right\rangle = \langle c_1\psi_1 +\delta_2\... ...rangle = c_1^2 E_1 + \delta_2^2 E_2 + \delta_3^2 E_3 + \ldots$$

Mul­ti­ply­ing the nor­mal­iza­tion con­di­tion by $E_1$ and sub­tract­ing it from the ex­pres­sion for the ex­pec­ta­tion en­ergy above gives the er­ror in en­ergy as:

$$\varepsilon \equiv \left\langle{E}\right\rangle -E_1 = \delta_2^2 (E_2-E_1) + \delta_3^2 (E_3-E_1) + \ldots$$

Note first that since all the terms in the right hand side are pos­i­tive, any ap­prox­i­mate wave func­tion has more ex­pec­ta­tion en­ergy than the ground state $E_1$. It does not have to be a sin­gle en­ergy eigen­func­tion of higher en­ergy. But that should not be a sur­prise.

Nor is it sur­pris­ing that the ex­pres­sion above shows that the er­ror in en­ergy $\varepsilon$ will be small if the co­ef­fi­cients $\delta_i$ of the in­cor­rect en­ergy eigen­func­tions are small and de­crease suit­ably in mag­ni­tude when $i$ in­creases.

How­ever, note that while the er­rors in wave func­tion are di­rectly pro­por­tional to the co­ef­fi­cients $\delta_i$, the er­ror in en­ergy is pro­por­tional to the squares of these co­ef­fi­cients. That makes the er­ror in en­ergy un­ex­pect­edly small, be­cause the square of any small quan­tity is much smaller still. (This as­sumes that the term small is de­fined in a mean­ing­ful nondi­men­sional way.)

That small er­ror in en­ergy is great be­cause the com­puted en­ergy is im­por­tant for a num­ber of things, like de­ter­min­ing whether a sta­ble ground state of the sup­posed form ex­ists in the first place, and if it does, how fast it in­ter­acts with other en­ergy eigen­func­tions if there is un­cer­tainty in en­ergy, chap­ter 7.

While it may seem ob­vi­ous that if the ap­prox­i­mate wave func­tion is close to the cor­rect one, then the ap­prox­i­mate en­ergy will be close to the cor­rect one, the re­verse is less triv­ial. If the ap­prox­i­mate en­ergy is close to the ex­act en­ergy, does that nec­es­sar­ily mean that en­tire wave func­tion is close to the ex­act one? For­tu­nately, the an­swer to that ques­tion is usu­ally yes.

In par­tic­u­lar, note from the ex­pres­sion for the er­ror in en­ergy above that for any co­ef­fi­cient $\delta_i$

$$\delta_i \le \sqrt{\frac{\varepsilon}{E_i-E_1}}$$

even in the worst-case sce­nario that all the er­ror is in the $i$-th term. From the above, the amount $\delta_i$ of each pol­lut­ing higher-en­ergy eigen­func­tion func­tion is small if $\varepsilon$ is small.

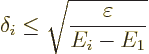
But do also note the ef­fect of the de­nom­i­na­tor. If it too is small, it may in­crease the pos­si­ble er­ror. The worst case oc­curs for the sec­ond low­est en­ergy state. If the sec­ond-low­est en­ergy $E_2$ is very close to the ground-state en­ergy $E_1$, un­usual good ac­cu­racy in en­ergy may be re­quired to en­sure that the ap­prox­i­mate wave func­tion is ac­cu­rate. (How­ever, if $E_2$ equals the ground state en­ergy, the sec­ond state is a ground state too; the ground state is then no longer unique. In that case the er­ror from some valid ground state is de­scribed by the third en­ergy state, not the sec­ond.)

Con­sider also the mag­ni­tude of the er­ror in the ap­prox­i­mate wave func­tion. It is de­fined as

$$\vert\vert\delta_2 \psi_2 + \delta_3 \psi_3 + \ldots\vert\vert = \sqrt{\delta_2^2+\delta_3^2 +\ldots}$$

This can be re­lated to the er­ror in en­ergy by not­ing that from its given ex­pres­sion

$$\varepsilon \mathrel{\raisebox{-.7pt}{$\leqslant$}}\delta_2^2 (E_2-E_1) + \delta_3^2 (E_2-E_1) + \ldots$$

since $E_i-E_1$ is at least as big as $E_2-E_1$. Com­par­ing the ex­pres­sions above shows that

$$\vert\vert\delta_2 \psi_2 + \delta_3 \psi_3 + \ldots\vert\v... ...aisebox{-.7pt}{$\leqslant$}}\sqrt{\frac{\varepsilon}{E_2-E_1}}$$

So if the er­ror in en­ergy $\varepsilon$ is small, the mag­ni­tude of the er­ror in the wave func­tion is too.

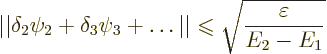
The bot­tom line is that the lower you can get your ex­pec­ta­tion en­ergy, the closer you will get to the true ground state en­ergy. In ad­di­tion the small er­ror in en­ergy will re­flect in a small er­ror in wave func­tion too.