| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.21 Solution of the hydrogen molecular ion
The key to the variational approximation to the hydrogen molecular ion
is to be able to accurately evaluate the expectation energy
This can be multiplied out and simplified by noting that 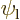 and
and
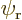 are eigenfunctions of the partial Hamiltonians. For example,
are eigenfunctions of the partial Hamiltonians. For example,
where 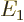 is the -13.6 eV hydrogen atom ground state energy.
The expression can be further simplified by noting that by symmetry
is the -13.6 eV hydrogen atom ground state energy.
The expression can be further simplified by noting that by symmetry
and that 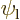 and
and 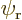 are real, so that the
left and right sides of the various inner products can be reversed.
Also,
are real, so that the
left and right sides of the various inner products can be reversed.
Also,  and
and 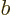 are related by the normalization requirement
are related by the normalization requirement
Cleaning up the expectation energy in this way, the result is
which includes the proton to proton repulsion energy (the 1
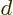 ). The
energy
). The
energy 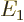 is the
is the  13.6 eV amount of energy when the protons are
far apart.
13.6 eV amount of energy when the protons are
far apart.
Numerical integration is not needed; the inner product integrals in
this expression can be done analytically. To do so, take the origin
of a spherical coordinate system  at the left proton,
and the axis towards the right one, so that
at the left proton,
and the axis towards the right one, so that
In those terms,
Then integrate angles first using 

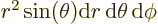

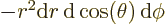 . Do not forget that
. Do not forget that

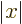 , not
, not  , e.g.
, e.g. 
 3, not
3, not  3. More details are in [25, pp. 305-307].
3. More details are in [25, pp. 305-307].
The overlap integral
turns out to be
and provides a measure of how much the regions of the two wave
functions overlap. The direct integral
is
and gives the classical potential of an electron density of strength
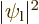 in the field of the right proton, except for the
factor
in the field of the right proton, except for the
factor 
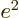

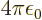 . The “exchange
integral” is
. The “exchange
integral” is
and is somewhat of a twilight term, since 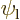 suggests that the
electron is around the left proton, but
suggests that the
electron is around the left proton, but 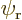 suggests it is around
the right one.
suggests it is around
the right one.
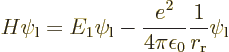
![\begin{eqnarray*}
\left\langle{E}\right\rangle &= & E_1 - \\
&& \frac{e^2}{4 ...
...r_{\rm {r}}^{-1} \psi_{\rm {l}} \right\rangle
\right\}
\right]
\end{eqnarray*}](img6252.gif)
![]()
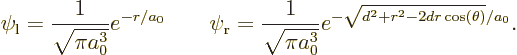
![\begin{displaymath}
\left\langle \psi_{\rm {l}} \vert\psi_{\rm {r}} \right\rang...
... + \frac{d}{a_0} + \frac13 \left(\frac{d}{a_0}\right)^2\right]
\end{displaymath}](img6259.gif)
![\begin{displaymath}
\left\langle \psi_{\rm {l}}\vert r_{\rm {r}}^{-1} \psi_{\rm...
...rac{1}{d} - \left[\frac{1}{a_0}+\frac{1}{d}\right] e^{-2d/a_0}
\end{displaymath}](img6260.gif)
![\begin{displaymath}
\left\langle \psi_{\rm {l}} \vert r_{\rm {l}}^{-1} \psi_{\r...
...gle
=
\left[\frac{1}{a_0}+\frac{d}{a_0^2}\right] e^{-d/a_0}.
\end{displaymath}](img6261.gif)