| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.20 Derivation of the commutator rules
This note explains where the formulae of chapter 4.5.4 come
from.
The general assertions are readily checked by simply writing out both
sides of the equation and comparing. And some are just rewrites of
earlier ones.
Position and potential energy operators commute since they are just
ordinary numerical multiplications, and these commute.
The linear momentum operators commute because the order in which
differentiation is done is irrelevant. Similarly, commutators between
angular momentum in one direction and position in another direction
commute since the other directions are not affected by the
differentiation.
The commutator between the position 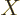 and linear momentum
and linear momentum 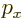 in
the
in
the  -direction was worked out in the previous subsection to
figure out Heisenberg's uncertainty principle. Of course,
three-dimensional space has no preferred direction, so the result applies
the same in any direction, including the
-direction was worked out in the previous subsection to
figure out Heisenberg's uncertainty principle. Of course,
three-dimensional space has no preferred direction, so the result applies
the same in any direction, including the  and
and  directions.
directions.
The angular momentum commutators are simplest obtained by just
grinding out
using the linear combination and product manipulation rules and the
commutators for linear angular momentum. To generalize the result you
get, you cannot just arbitrarily swap  ,
,  , and
, and
 , since, as every mechanic knows, a right-handed screw is not
the same as a left-handed one, and some axes swaps would turn one into
the other. But you can swap axes according to the
, since, as every mechanic knows, a right-handed screw is not
the same as a left-handed one, and some axes swaps would turn one into
the other. But you can swap axes according to the
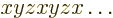 ” “cyclic permutation
” “cyclic permutation
scheme, as in:
which produces the other two commutators if you do it twice:
For the commutators with square angular momentum, work out
using the manipulation rules and the commutators between angular
momentum components.
A commutator like ![$[{\widehat x},\L _x]$](img6218.gif)

![$[{\widehat x},{\widehat y}{\widehat p}_z-{\widehat z}{\widehat p}_y]$](img6219.gif) is zero
because everything commutes in it. However, in a commutator like
is zero
because everything commutes in it. However, in a commutator like
![$[{\widehat x},\L _y]$](img6220.gif)

![$[{\widehat x},{\widehat z}{\widehat p}_x-{\widehat x}{\widehat p}_z]$](img6221.gif) ,
,  does not commute
with
does not commute
with 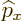 , so multiplying out and taking the
, so multiplying out and taking the 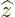 out of
out of
![$[{\widehat x},{\widehat z}{\widehat p}_x]$](img6222.gif) at its own side, you get
at its own side, you get ![${\widehat z}[{\widehat x},{\widehat p}_x]$](img6223.gif) , and the
commutator left is the canonical one, which has value
, and the
commutator left is the canonical one, which has value
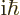 . Plug these results and similar into
. Plug these results and similar into
![$[{\widehat x}^2+{\widehat y}^2+{\widehat z}^2,L_x]$](img6224.gif) and you get zero.
and you get zero.
For a commutator like ![$[{\widehat x},\L ^2]$](img6225.gif)

![$[{\widehat x},\L _x^2+\L _y^2+\L _z^2]$](img6226.gif) , the
, the 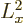 term produces zero
because
term produces zero
because 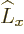 commutes with
commutes with  , and in the remaining term,
taking the various factors out at their own sides of the commutator
produces
, and in the remaining term,
taking the various factors out at their own sides of the commutator
produces
the final equality because of the commutators already worked out. Now
by the nature of the commutator, you can swap the order of the terms
in 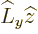 as long as you add the commutator
as long as you add the commutator ![$[\L _y,{\widehat z}]$](img6230.gif) to make up
for it, and that commutator was already found to be
to make up
for it, and that commutator was already found to be
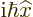 , The same way the order of
, The same way the order of 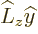 can be swapped
to give
can be swapped
to give
and the parenthetical expression can be recognized as the
 -component of
-component of 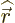

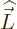 , giving one of the
expressions claimed.
, giving one of the
expressions claimed.
Instead you can work out the parenthetical expression further by
substituting in the definitions for  and
and 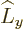 :
:
where the third term added within the big parentheses is
self-evidently zero. This can be reordered to the  -component of
the second claimed expression. And as always, the other components
are of course no different.
-component of
the second claimed expression. And as always, the other components
are of course no different.
The commutators between linear and angular momentum go almost
identically, except for additional swaps in the order between position
and momentum operators using the canonical commutator.
To derive the first commutator in (4.73), consider the
 -component as the example:
-component as the example:
because  commutes with
commutes with 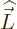 , and using
(4.68)
, and using
(4.68)
Now use the commutator ![$[\L _y,\L _z]$](img6238.gif) to get rid of
to get rid of 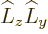 and
and
![$[\L _z,\L _x]$](img6240.gif) to get rid of
to get rid of 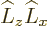 and clean up to get
and clean up to get
Now 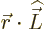

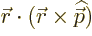
 0 so
0 so
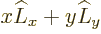

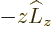 , which gives the claimed
expression. To verify the second equation of (4.73),
use (4.68), the first of (4.73), and
the definition of
, which gives the claimed
expression. To verify the second equation of (4.73),
use (4.68), the first of (4.73), and
the definition of ![$[{\skew0\vec r},\L ^2]$](img6247.gif) .
.
![]()
![]()
![]() -
-![]()
![]()
”
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![\begin{eqnarray*}[{\widehat x},\L ^2]
& = & \L _y[{\widehat x},\L _y] + [{\wide...
... {\rm i}\hbar \L _z {\widehat y}- {\rm i}\hbar {\widehat y}\L _z
\end{eqnarray*}](img6228.gif)
![]()
![]() :
:![]() -
-