| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.73 Orbital motion in a magnetic field
This note derives the energy of a charged particle in an external
magnetic field. The field is assumed constant.
According to chapter 13.1, the Hamiltonian is
where  and
and  are the mass and charge of the particle and the
vector potential
are the mass and charge of the particle and the
vector potential  is related to the magnetic field
is related to the magnetic field 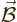 by
by 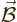



 . The potential energy
. The potential energy  is of
no particular interest in this note. The first term is, and it can be
multiplied out as:
is of
no particular interest in this note. The first term is, and it can be
multiplied out as:
The middle two terms in the right hand side are the changes in the
Hamiltonian due to the magnetic field; they will be denoted as:
Now to simplify the analysis, align the  -axis with
-axis with 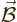 so that
so that
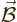

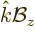 . Then an appropriate vector
potential
. Then an appropriate vector
potential  is
is
The vector potential is not unique, but a check shows that indeed




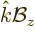

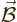 for the one
above. Also, the canonical momentum is
for the one
above. Also, the canonical momentum is
Therefore, in the term 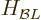 above,
above,
the latter equality being true because of the definition of angular
momentum as 

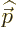 . Because the
. Because the  -axis was
aligned with
-axis was
aligned with 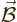 ,
, 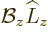

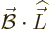 , so,
finally,
, so,
finally,
Similarly, in the part 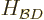 of the Hamiltonian, substitution of
the expression for
of the Hamiltonian, substitution of
the expression for  produces
produces
or writing it so that it is independent of how the  -axis is
aligned,
-axis is
aligned,
![]() -
-![]()
![]()
![]()
![]() .
.![]()
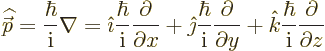
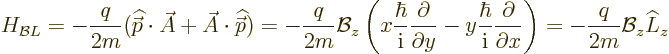
![]()
![]()