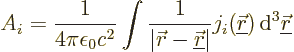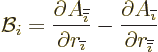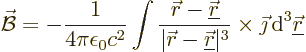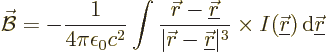| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
D.72 Various electrostatic derivations.
This section gives various derivations for the electromagnetostatic
solutions of chapter 13.3.
D.72.1 Existence of a potential
This subsection shows that if the curl of the electric field  (or of any other vector field, like the magnetic one or a force
field), is zero, it is minus the gradient of some potential.
(or of any other vector field, like the magnetic one or a force
field), is zero, it is minus the gradient of some potential.
That potential can be defined to be
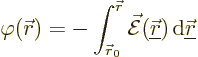 |
(D.47) |
where 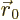 is some arbitrarily chosen reference point. You might
think that the value of
is some arbitrarily chosen reference point. You might
think that the value of 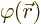 would depend on what
integration path you took from the reference point to
would depend on what
integration path you took from the reference point to  , but
the Stokes’ theorem of calculus says that the difference between
integrals leading to the same path must be zero since
, but
the Stokes’ theorem of calculus says that the difference between
integrals leading to the same path must be zero since 

 is zero.
is zero.
Now if you evaluate  at a neighboring point
at a neighboring point
 by a path first going to
by a path first going to  and from there
straight to
and from there
straight to 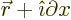 , the difference in integrals
is just the integral over the final segment:
, the difference in integrals
is just the integral over the final segment:
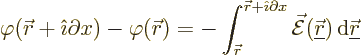 |
(D.48) |
Dividing by 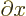 and then taking the limit
and then taking the limit 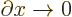 shows that minus the
shows that minus the  -derivative of
-derivative of  gives the
gives the
 -component of the electric field. The same of course for the other
components, since the
-component of the electric field. The same of course for the other
components, since the  -direction is arbitrary.
-direction is arbitrary.
Note that if regions are multiply connected, the potential may not be
quite unique. The most important example of that is the magnetic
potential of an infinite straight electric wire. Since the curl of
the magnetic field is nonzero inside the wire, the path of integration
must stay clear of the wire. It then turns out that the value of the
potential depends on how many times the chosen integration path wraps
around the wire. Indeed, the magnetic potential is 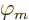



 . and as you know, an angle
like
. and as you know, an angle
like  is indeterminate by any integer multiple of
is indeterminate by any integer multiple of
 .
.
D.72.2 The Laplace equation
The homogeneous Poisson equation,
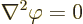 |
(D.49) |
for some unknown function  is called the Laplace equation.
It is very important in many areas of physics and engineering. This
note derives some of its generic properties.
is called the Laplace equation.
It is very important in many areas of physics and engineering. This
note derives some of its generic properties.
The so-called mean-value property says that the average of  over the surface of any sphere in which the Laplace equation holds is
the value of
over the surface of any sphere in which the Laplace equation holds is
the value of  at the center of the sphere. To see why,
for convenience take the center of the sphere as the origin of a
spherical coordinate system. Now
at the center of the sphere. To see why,
for convenience take the center of the sphere as the origin of a
spherical coordinate system. Now
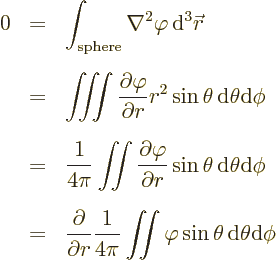
the first equality since  satisfies the Laplace equation,
the second because of the divergence theorem, the third because the
integral is zero, so a constant factor does not make a difference, and
the fourth by changing the order of integration and differentiation.
It follows that the average of
satisfies the Laplace equation,
the second because of the divergence theorem, the third because the
integral is zero, so a constant factor does not make a difference, and
the fourth by changing the order of integration and differentiation.
It follows that the average of  is the same on all
spherical surfaces centered around the origin. Since this includes
as a limiting case the origin and the average of
is the same on all
spherical surfaces centered around the origin. Since this includes
as a limiting case the origin and the average of  over the
single point at the origin is just
over the
single point at the origin is just  at the origin,
the mean value property follows.
at the origin,
the mean value property follows.
The so called maximum-minimum principle says that either  is
constant everywhere or its maximum and minimum are on a boundary or at
infinity. The reason is the mean-value property above. Suppose there
is an absolute maximum in the interior of the region in which the
Laplace equation applies. Enclose the maximum by a small sphere.
Since the values of
is
constant everywhere or its maximum and minimum are on a boundary or at
infinity. The reason is the mean-value property above. Suppose there
is an absolute maximum in the interior of the region in which the
Laplace equation applies. Enclose the maximum by a small sphere.
Since the values of  would be less than the maximum on the
surface of the sphere, the average value on the surface must be less
than the maximum too. But the mean value theorem says it must be the
same. The only way around that is if
would be less than the maximum on the
surface of the sphere, the average value on the surface must be less
than the maximum too. But the mean value theorem says it must be the
same. The only way around that is if  is completely constant
in the sphere, but then the
is completely constant
in the sphere, but then the maximum
is not a true
maximum. And then you can start sphere-hopping
to
show that  is constant everywhere. Minima go the same way.
is constant everywhere. Minima go the same way.
The only solution of the Laplace equation in all of space that is zero
at infinity is zero everywhere. In more general regions, as long as
the solution is zero on all boundaries, including infinity where
relevant, then the solution is zero everywhere. The reason is the
maximum-minimum principle: if there was a point where the solution was
positive/negative, then there would have to be an interior
maximum/minimum somewhere.
The solution of the Laplace equation for given boundary values is
unique. The reason is that the difference between any two solutions
must satisfy the Laplace equation with zero boundary values, hence
must be zero.
D.72.3 Egg-shaped dipole field lines
The egg shape of the ideal dipole field lines can be found by assuming
that the dipole is directed along the  -axis. Then the field
lines in the
-axis. Then the field
lines in the 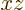 -plane satisfy
-plane satisfy
Change to a new variable 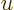 by replacing
by replacing  by
by 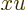 to get:
to get:
Integrating and replacing 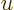 again by
again by 

 gives
gives
where 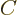 represents the integration constant from the integration.
Near the origin,
represents the integration constant from the integration.
Near the origin, 
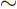
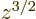

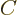 ; therefore the field
line has infinite curvature at the origin, explaining the pronounced
egg shape. Rewritten in spherical coordinates, the field lines are
given by
; therefore the field
line has infinite curvature at the origin, explaining the pronounced
egg shape. Rewritten in spherical coordinates, the field lines are
given by 

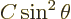 and
and  constant, and that is
also valid outside the
constant, and that is
also valid outside the 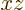 -plane.
-plane.
D.72.4 Ideal charge dipole delta function
Next is the delta function in the electric field generated by a charge
distribution that is contracted to an ideal dipole. To find the
precise delta function, the electric field can be integrated over a
small sphere, but still large enough that on its surface the ideal
dipole potential is valid. The integral will give the strength of the
delta function. Since the electric field is minus the gradient of the
potential, an arbitrary component 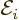 integrates to
integrates to
where 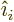 is the unit vector in the
is the unit vector in the  -direction and the
divergence theorem of calculus was used to convert the integral to an
integral over the surface area
-direction and the
divergence theorem of calculus was used to convert the integral to an
integral over the surface area  of the sphere. Noting that the
vector
of the sphere. Noting that the
vector  normal to the surface of the sphere equals
normal to the surface of the sphere equals


 , and that the potential is the ideal dipole one,
you get
, and that the potential is the ideal dipole one,
you get
For simplicity, take the  -axis along the dipole moment; then
-axis along the dipole moment; then
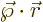

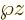 . For the
. For the  -component
-component
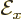 ,
, 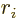

 so that the integrand is proportional
to
so that the integrand is proportional
to 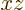 , and that integrates to zero over the surface of the
sphere because the negative
, and that integrates to zero over the surface of the
sphere because the negative  -values cancel the positive ones
at the same
-values cancel the positive ones
at the same  . The same for the
. The same for the  -component of the
field, so only the
-component of the
field, so only the  -component, or more generally, the
component in the same direction as
-component, or more generally, the
component in the same direction as 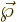 , has a delta
function. For
, has a delta
function. For 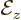 , you are integrating
, you are integrating 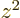 , and by
symmetry that is the same as integrating
, and by
symmetry that is the same as integrating 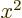 or
or 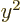 , so it
is the same as integrating
, so it
is the same as integrating  . Since the surface of
the sphere equals
. Since the surface of
the sphere equals 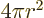 , the delta function included in
the expression for the field of a dipole as listed in table
13.2 is obtained.
, the delta function included in
the expression for the field of a dipole as listed in table
13.2 is obtained.
D.72.5 Integrals of the current density
In subsequent derivations, various integrals of the current density
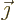 are needed. In all cases it is assumed that the current
density vanishes strongly outside some region. Of course, normally an
electric motor or electromagnet has electrical leads going towards and
away from of it; it is assumed that these are stranded so tightly
together that their net effect can be ignored.
are needed. In all cases it is assumed that the current
density vanishes strongly outside some region. Of course, normally an
electric motor or electromagnet has electrical leads going towards and
away from of it; it is assumed that these are stranded so tightly
together that their net effect can be ignored.
Consider an integral like  where
where  is any component
is any component 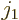 ,
, 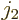 , or
, or 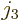 of the current
density,
of the current
density, 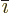 is the index following
is the index following  in the sequence
in the sequence
 ,
,  and
and  are nonnegative integers, and
the integration is over all of space. By integration by parts in the
are nonnegative integers, and
the integration is over all of space. By integration by parts in the
 -direction, and using the fact that the current densities
vanish at infinity,
-direction, and using the fact that the current densities
vanish at infinity,
Now use the fact that the divergence of the current density is zero
since the charge density is constant for electromagnetostatic
solutions:
where 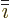 is the index preceding
is the index preceding  in the sequence
in the sequence
 . The final integral can be integrated in
the
. The final integral can be integrated in
the 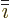 -direction and is then seen to be zero because
-direction and is then seen to be zero because
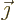 vanishes at infinity.
vanishes at infinity.
The first integral in the right hand side can be integrated by parts
in the 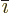 -direction to give the final result:
-direction to give the final result:
 |
(D.50) |
It follows from this equation with 
 0,
0, 
 1 that
1 that
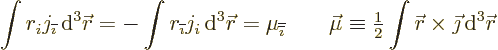 |
(D.51) |
with  the current distribution’s dipole moment. In these
expressions, you can swap indices as
the current distribution’s dipole moment. In these
expressions, you can swap indices as
because only the relative ordering of the indices in the sequence
 is relevant.
is relevant.
In quantum applications, it is often necessary to relate the dipole
moment to the angular momentum of the current carriers. Since the
current density is the charge per unit volume times its velocity, you
get the linear momentum per unit volume by multiplying by the ratio
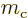

 of current carrier mass over charge. Then the
angular momentum is
of current carrier mass over charge. Then the
angular momentum is
D.72.6 Lorentz forces on a current distribution
Next is the derivation of the Lorentz forces on a given current
distribution 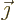 in a constant external magnetic field
in a constant external magnetic field
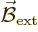 . The Lorentz force law says that the force
. The Lorentz force law says that the force
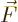 on a charge
on a charge  moving with speed
moving with speed  equals
equals
In terms of a current distribution, the moving charge per unit volume
times its velocity is the current density, so the force on a volume
element 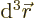 is:
is:
The net force on the current distribution is therefore zero, because
according to (D.50) with 


 0, the integrals of the
components of the current distribution are zero.
0, the integrals of the
components of the current distribution are zero.
The moment is not zero, however. It is given by
According to the vectorial triple product rule, that is
The second integral is zero because of (D.50) with

 1,
1, 
 0. What is left is can be written in index notation as
0. What is left is can be written in index notation as
The first of the three integrals is zero because of (D.50)
with 
 1,
1, 
 0. The other two can be rewritten using
(D.51):
0. The other two can be rewritten using
(D.51):
and in vector notation that reads
When the (frozen) current distribution is slowly rotated around the
axis aligned with the moment vector, the work done is
where  is the angle between
is the angle between  and
and
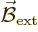 . By integration, it follows that the work done
corresponds to a change in energy for an energy given by
. By integration, it follows that the work done
corresponds to a change in energy for an energy given by
D.72.7 Field of a current dipole
A current density 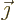 creates a magnetic field because of
Maxwell’s second and fourth equations for the divergence and curl
of the magnetic field:
creates a magnetic field because of
Maxwell’s second and fourth equations for the divergence and curl
of the magnetic field:
where 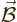 vanishes at infinity assuming there is no additional
ambient magnetic field.
vanishes at infinity assuming there is no additional
ambient magnetic field.
A magnetic vector potential  will now be defined as the
solution of the Poisson equation
will now be defined as the
solution of the Poisson equation
that vanishes at infinity. Taking the divergence of this equation
shows that the divergence of the vector potential satisfies a
homogeneous Poisson equation, because the divergence of the current
density is zero, with zero boundary conditions at infinity. Therefore
the divergence of the vector potential is zero. It then follows that
because it satisfies the equations for 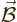 : the divergence of
any curl is zero, and the curl of the curl of the vector potential is
according to the vectorial triple product its Laplacian, hence the
correct curl of the magnetic field.
: the divergence of
any curl is zero, and the curl of the curl of the vector potential is
according to the vectorial triple product its Laplacian, hence the
correct curl of the magnetic field.
You might of course wonder whether there might not be more than one
magnetic field that has the given divergence and curl and is zero at
infinity. The answer is no. The difference between any two such
fields must have zero divergence and curl. Therefore the curl of the
curl of the difference is zero too, and the vectorial triple product
shows that equal to minus the Laplacian of the difference. If the
Laplacian of the difference is zero, then the difference is zero,
since the difference is zero at infinity (subsection 2). So the
solutions must be the same.
Since the integrals of the current density are zero, (D.50)
with 


 0, the asymptotic expansion (13.31) of the
Green’s function integral shows that at large distances, the
components of
0, the asymptotic expansion (13.31) of the
Green’s function integral shows that at large distances, the
components of  behave as a dipole potential. Specifically,
behave as a dipole potential. Specifically,
Now the term 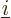

 in the sum does not give a contribution, because
of (D.50) with
in the sum does not give a contribution, because
of (D.50) with 
 1,
1, 
 0. The other two terms are
0. The other two terms are
with 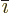 following
following  in the sequence
in the sequence  and
and
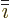 preceding it. These two integrals can be rewritten using
(D.51) to give
preceding it. These two integrals can be rewritten using
(D.51) to give
Note that the expression between brackets is just the  -th
component of
-th
component of 

 .
.
The magnetic field is the curl of  , so
, so
and substituting in for the vector potential from above,
differentiating, and cleaning up produces
This is the same asymptotic field as a charge dipole with strength
 would have.
would have.
However, for an ideal current dipole, the delta function at the origin
will be different than that derived for a charge dipole in the first
subsection. Integrate the magnetic field over a sphere large enough
that on its surface, the asymptotic field is accurate:
Using the divergence theorem, the right hand side becomes an
integral over the surface of the sphere:
Substituting in the asymptotic expression for 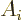 above,
above,
The integrals of 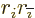 and
and  are zero, for one
because the integrand is odd in
are zero, for one
because the integrand is odd in 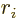 . The integrals of
. The integrals of
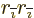 and
and  are each one third of the
integral of
are each one third of the
integral of 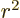 because of symmetry. So, noting that the surface
area
because of symmetry. So, noting that the surface
area  of the spherical surface is
of the spherical surface is 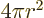 ,
,
That gives the strength of the delta function for an ideal current
dipole.
D.72.8 Biot-Savart law
In the previous section, it was noted that the magnetic field of a
current distribution is the curl of a vector potential  .
This vector potential satisfies the Poisson equation
.
This vector potential satisfies the Poisson equation
The solution for the vector potential can be written explicitly in
terms of the current density using the Green’s function integral
(13.29):
The magnetic field is the curl of  ,
,
or substituting in and differentiating under the integral
In vector notation that gives the Biot-Savart law
Now assume that the current distribution is limited to one or more
thin wires, as it usually is. In that case, a volume element of
nonzero current distribution can be written as
where in the right hand side 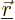 describes the position of the
centerline of the wire and
describes the position of the
centerline of the wire and  is the current through the wire. More
specifically,
is the current through the wire. More
specifically,  is the integral of the current density over the
cross section of the wire. The Biot-Savart law becomes
is the integral of the current density over the
cross section of the wire. The Biot-Savart law becomes
where the integration is over all infinitesimal segments
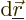 of the wires.
of the wires.
![]()
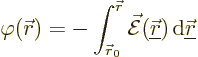
![]()
![]()
![]()
![]() ,
,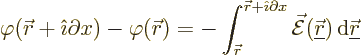
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
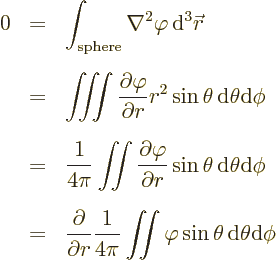
![]()
![]()
![]()
![]()
![]() -
-![]() -
-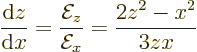

![]()
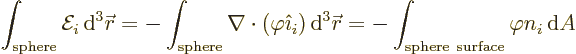
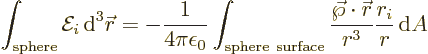
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() -
-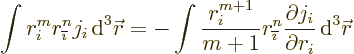
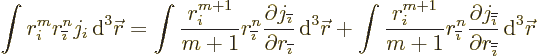
![]() -
-![]()
![]()
![]()
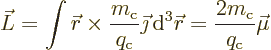
![]()
![]() .
.![]()
![]()
![]()
![]()
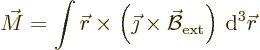
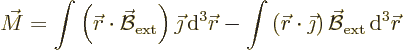
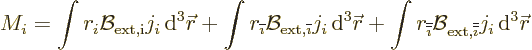
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![\begin{displaymath}
A_i \sim \frac{1}{4\pi\epsilon_0c^2r^3}
\left[
r_{\overli...
...ne{\imath}}}j_i {\,\rm d}^3{\underline{\skew0\vec r}}
\right]
\end{displaymath}](img7457.gif)
![]() ,
,

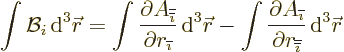
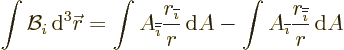
![\begin{displaymath}
\int {\cal B}_i {\,\rm d}^3{\skew0\vec r}= - \frac{1}{4\pi\...
...\imath}}}) r_{\overline{\overline{\imath}}}{\,\rm d}A
\right]
\end{displaymath}](img7463.gif)
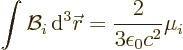
![]() .
.