| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.52 Simplification of the Hartree-Fock energy
This note derives the expectation energy for a wave function given by
a single Slater determinant.
First note that if you multiply out a Slater determinant
you are going to get terms, or Hartree products if you want, of the
form
where the numbers 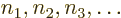 of the single-electron states
can have values from 1 to
of the single-electron states
can have values from 1 to  , but they must be all different. So there are
, but they must be all different. So there are 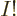 such terms: there are
such terms: there are  possibilities among
possibilities among 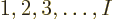 for the number
for the number 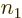 of the
single-electron state for electron 1, which leaves
of the
single-electron state for electron 1, which leaves  remaining
possibilities for the number
remaining
possibilities for the number 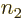 of the single-electron state for
electron 2,
of the single-electron state for
electron 2,  remaining possibilities for
remaining possibilities for 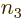 ,
etcetera. That means a total of
,
etcetera. That means a total of 

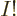 terms. As far as the sign of the term is concerned, just don't worry
about it. The only thing to remember is that whenever you exchange
two
terms. As far as the sign of the term is concerned, just don't worry
about it. The only thing to remember is that whenever you exchange
two  values, it changes the sign of the term. It has to be,
because exchanging
values, it changes the sign of the term. It has to be,
because exchanging  values is equivalent to exchanging electrons,
and the complete wave function must change sign under that.
values is equivalent to exchanging electrons,
and the complete wave function must change sign under that.
To make the above more concrete, consider the example of a Slater
determinant of three single-electron functions. It writes out to,
taking 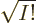 to the other side for convenience,
to the other side for convenience,
The first two rows in the expansion cover the possibility that 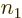
 1, with the first one the possibility that
1, with the first one the possibility that 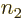
 2 and the
second one the possibility that
2 and the
second one the possibility that 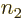
 3; note that then there
are no choices left for
3; note that then there
are no choices left for 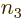 . Similarly the second two rows cover
the two possibilities that
. Similarly the second two rows cover
the two possibilities that 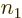
 2, and the third that
2, and the third that 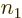
 3. You see that there are 3! = 6 Hartree product terms total.
3. You see that there are 3! = 6 Hartree product terms total.
Next, recall that the Hamiltonian consists of single-electron
Hamiltonians 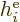 and electron-pair repulsion potentials
and electron-pair repulsion potentials
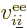 . The expectation value of a single electron
Hamiltonian
. The expectation value of a single electron
Hamiltonian 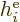 will be done first. In forming the inner product
will be done first. In forming the inner product
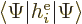 , and taking
, and taking  apart into
its Hartree product terms as above, you are going to end up with a
large number of individual terms that all look like
apart into
its Hartree product terms as above, you are going to end up with a
large number of individual terms that all look like
Note that overlines will be used to distinguish the wave function in
the right hand side of the inner product from the one in the left hand
side. Also note that to take this inner product, you have to
integrate over  scalar position coordinates, and sum over
scalar position coordinates, and sum over  spin
values.
spin
values.
But multiple integrals, and sums, can be factored into single
integrals, and sums, as long as the integrands and limits only involve
single variables. So you can factor out the inner product as
Now you can start the weeding-out process, because the single-electron
functions are orthonormal. So factors in this product are zero unless
all of the following requirements are met:
Note that
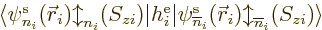 does not require
does not require 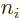

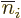 for a nonzero value,
since the single-electron functions are most definitely not
eigenfunctions of the single-electron Hamiltonians, (you would wish
things were that easy!) But now remember that the numbers
for a nonzero value,
since the single-electron functions are most definitely not
eigenfunctions of the single-electron Hamiltonians, (you would wish
things were that easy!) But now remember that the numbers
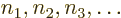 in an individual term are all different. So the
numbers
in an individual term are all different. So the
numbers 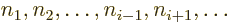 include all the
numbers that are not equal to
include all the
numbers that are not equal to 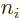 . Then so do
. Then so do
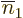 ,
, 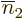 , ...,
, ...,
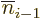 ,
, 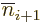 ,..., because they
are the same. And since
,..., because they
are the same. And since 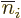 must be different from all
of those, it can only be equal to
must be different from all
of those, it can only be equal to 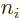 anyway.
anyway.
So what is left? Well, with all the 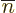 values equal to the
corresponding
values equal to the
corresponding  values, all the plain inner products are one on
account of orthonormality, and the only thing left is:
values, all the plain inner products are one on
account of orthonormality, and the only thing left is:
Also, the two signs are equal, because with all the 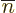 values equal to the corresponding
values equal to the corresponding  values, the wave function term
in the right side of the inner product is the exact same one as in the
left side. So the signs multiply to 1, and you can further factor out
the spin inner product, which is one since the spin states are
normalized:
values, the wave function term
in the right side of the inner product is the exact same one as in the
left side. So the signs multiply to 1, and you can further factor out
the spin inner product, which is one since the spin states are
normalized:
where for brevity the remaining inner product was called
 . Normally you would call it
. Normally you would call it 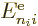 , but
an inner product integral does not care what the integration variable
is called, so the thing has the same value regardless what the
electron
, but
an inner product integral does not care what the integration variable
is called, so the thing has the same value regardless what the
electron  is. Only the value of the single-electron function
number
is. Only the value of the single-electron function
number 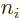

 makes a difference.
makes a difference.
Next, how many such terms are there for a given electron  and
single-electron function number
and
single-electron function number  ? Well, for a given
? Well, for a given  value for electron
value for electron  , there are
, there are  possible values left
among
possible values left
among 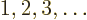 for the
for the  value of the first of the other
electrons, then
value of the first of the other
electrons, then  left for the second of the other electrons,
etcetera. So there are a total of
left for the second of the other electrons,
etcetera. So there are a total of 

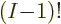 such terms. Since
such terms. Since 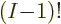

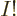
 1/
1/ , if you
sum them all together you get a total contribution from terms in which
electron
, if you
sum them all together you get a total contribution from terms in which
electron  is in state
is in state  equal to
equal to 

 . Summing
over the
. Summing
over the  electrons kills off the factor 1
electrons kills off the factor 1
 and so you finally
get the total energy due to the single-electron Hamiltonians as
and so you finally
get the total energy due to the single-electron Hamiltonians as
You might have guessed that answer from the start. Since the inner
product integral is the same for all electrons, the subscripts  have been omitted.
have been omitted.
The good news is that the reasoning to get the Coulomb and exchange
contributions is pretty much the same. A single electron to electron
repulsion term 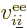 between an electron numbered
between an electron numbered  and
another numbered
and
another numbered 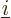 makes a contribution to the expectation energy
equal to
makes a contribution to the expectation energy
equal to 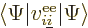 , and if you
multiply out
, and if you
multiply out  , you get terms of the general form:
, you get terms of the general form:
You can again split into a product of individual inner products,
except that you cannot split between electrons  and
and 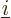 since
since
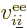 involves both electrons in a nontrivial way. Still,
you get again that all the other
involves both electrons in a nontrivial way. Still,
you get again that all the other  values must be the same as the
corresponding
values must be the same as the
corresponding 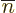 values, eliminating those inner products
from the expression:
values, eliminating those inner products
from the expression:
For given values of 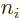 and
and 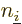 , there are
, there are 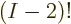 equivalent terms, since that is the number of possibilities left for
the
equivalent terms, since that is the number of possibilities left for
the 

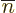 -values of the other
-values of the other  electrons.
electrons.
Next, 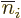 and
and 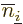 must together be the
same pair of numbers as
must together be the
same pair of numbers as 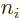 and
and 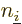 , since they
must be the two numbers left by the set of numbers not equal to
, since they
must be the two numbers left by the set of numbers not equal to 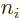 and
and 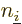 . But that still leaves two possibilities, they can
be in the same order or in reversed order:
. But that still leaves two possibilities, they can
be in the same order or in reversed order:
The first possibility gives rise to the Coulomb terms, the second to
the exchange ones. Note that the former case represents an inner
product involving a Hartree product with itself, and the latter case
an inner product of a Hartree product with the Hartree product that is
the same save for the fact that it has 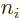 and
and 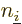 reversed,
or equivalently, electrons
reversed,
or equivalently, electrons  and
and 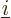 exchanged.
exchanged.
Consider the Coulomb terms first. For those the two Hartree products
in the inner product are the same, so their signs multiply to one.
Also, their spin states will be the same, so that inner product will
be one too. And as noted there are 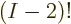 equivalent terms for
given
equivalent terms for
given 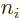 and
and 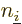 , so for each pair of electrons
, so for each pair of electrons  and
and
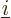
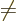
 , and each pair of states
, and each pair of states 

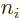 and
and
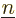

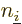 , you get one term
, you get one term
with
Again, the  are the same regardless of what
are the same regardless of what  and
and 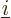 are; they depend only on what
are; they depend only on what 

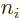 and
and 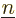

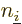 are. So the subscripts
are. So the subscripts  and
and 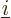 were left out, after setting
were left out, after setting


 and
and 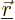

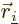 .
.
You now need to sum over all pairs of electrons with 
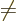
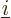 and pairs of single-electron function numbers
and pairs of single-electron function numbers 
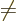
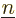 .
Since there are a total of
.
Since there are a total of 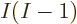 electron pairs, it takes out the
factor 1/
electron pairs, it takes out the
factor 1/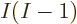 , and you get a contribution to the energy
, and you get a contribution to the energy
The factor 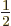 was added since for every electron pair, you are
summing both
was added since for every electron pair, you are
summing both 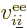 and
and 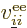 , and that
counts the same energy twice.
, and that
counts the same energy twice.
The exchange integrals go exactly the same way; the only differences
are that the Hartree product in the right hand side of the inner
product has the values of 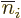 and
and 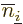 reversed, producing a change of sign, and that the inner product of
the spins is not trivial. Define
reversed, producing a change of sign, and that the inner product of
the spins is not trivial. Define
and then the total contribution is
Finally, you can leave the constraint 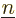
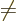
 on the sums away
since
on the sums away
since 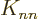

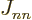 , so they cancel each other.
, so they cancel each other.
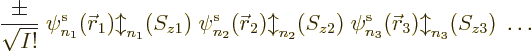
![]()
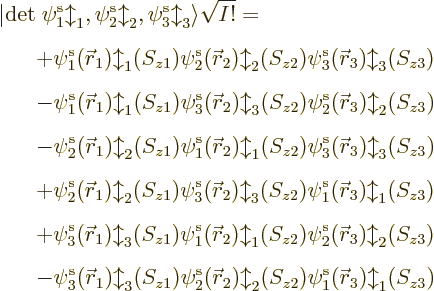
![]()
![]() .
.![]()
![]() ,
,![]()
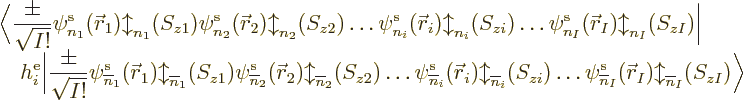
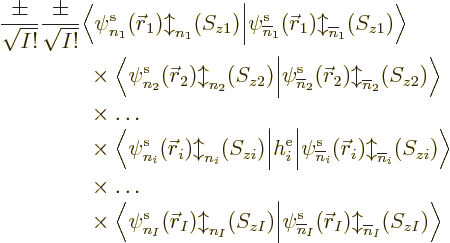
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]() ?
?![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()

![]()
![]()
![]()
![]() ,
,![]() ,
,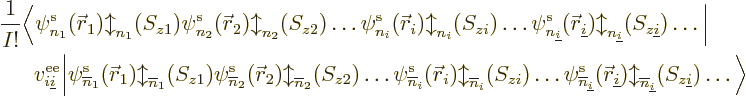
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() ,
,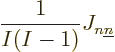
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,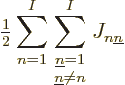
![]()
![]()
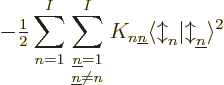
![]()
![]()
![]()
![]()
![]()
![]() ,
,