| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
N.16 A single Slater determinant is not exact
The simplest example that illustrates the problem with representing a
general wave function by a single Slater determinant is to try to
write a general two-variable function 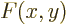 as a Slater determinant
of two functions
as a Slater determinant
of two functions 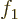 and
and 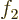 . You would write
. You would write
A general function 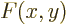 cannot be written as a combination of the
same two functions
cannot be written as a combination of the
same two functions 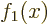 and
and 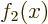 at every value
of
at every value
of  . However well chosen the two functions are.
. However well chosen the two functions are.
In fact, for a general antisymmetric function  , a single
Slater determinant can get
, a single
Slater determinant can get  right at only two nontrivial values
right at only two nontrivial values 

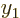 and
and 

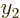 . (Nontrivial here means that
functions
. (Nontrivial here means that
functions 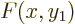 and
and 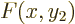 should not just be multiples of
each other.) Just take
should not just be multiples of
each other.) Just take 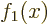

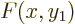 and
and 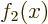

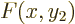 . You might object that in general, you have
. You might object that in general, you have
where 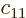 ,
,  ,
, 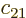 , and
, and  are
some constants. (They are
are
some constants. (They are 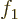 or
or 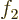 values at
values at 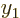 or
or
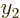 , to be precise). But if you plug these two expressions
into the Slater determinant formed with
, to be precise). But if you plug these two expressions
into the Slater determinant formed with 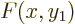 and
and 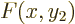 and
multiply out, you get the Slater determinant formed with
and
multiply out, you get the Slater determinant formed with 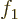 and
and
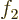 within a constant, so it makes no difference.
within a constant, so it makes no difference.
If you add a second Slater determinant, you can get  right at two
more
right at two
more  values
values 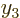 and
and 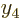 . Just take the second Slater
determinant's functions to be
. Just take the second Slater
determinant's functions to be 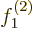

 and
and
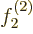

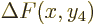 , where
, where 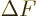 is the
deviation between the true function and what the first Slater
determinant gives. Keep adding Slater determinants to get more and
more
is the
deviation between the true function and what the first Slater
determinant gives. Keep adding Slater determinants to get more and
more  -values right. Since there are infinitely many
-values right. Since there are infinitely many
 -values to get right, you will in general need infinitely
many determinants.
-values to get right, you will in general need infinitely
many determinants.
You might object that maybe the deviation 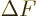 from the single
Slater determinant must be zero for some reason. But you can use the
same ideas to explicitly construct functions
from the single
Slater determinant must be zero for some reason. But you can use the
same ideas to explicitly construct functions  that show that this
is untrue. Just select two arbitrary but different functions
that show that this
is untrue. Just select two arbitrary but different functions 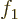 and
and 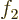 and form a Slater determinant. Now choose two locations
and form a Slater determinant. Now choose two locations
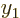 and
and 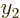 so that
so that  and
and 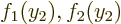 are not in the same ratio to each other. Then add additional Slater
determinants whose functions
are not in the same ratio to each other. Then add additional Slater
determinants whose functions
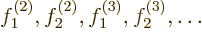 you choose so that
they are zero at
you choose so that
they are zero at 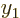 and
and 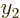 . The so constructed function
. The so constructed function
 is different from just the first Slater determinant. However, if
you try to describe this
is different from just the first Slater determinant. However, if
you try to describe this  by a single determinant, then it could
only be the first determinant since that is the only single
determinant that gets
by a single determinant, then it could
only be the first determinant since that is the only single
determinant that gets 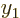 and
and 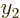 right. So a single determinant
cannot get
right. So a single determinant
cannot get  right.
right.
![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() -
-![]() -
-![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()