| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
N.17 Generalized orbitals
This note has a brief look at generalized orbitals of the form
For such orbitals, the expectation energy can be worked out in exactly
the same way as in {D.52}, except without simplifying
the spin terms. The energy is
To multiply out to the individual spin terms, it is convenient to
normalize the spatial functions, and write
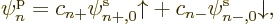
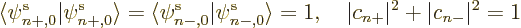
In that case, the expectation energy multiplies out to
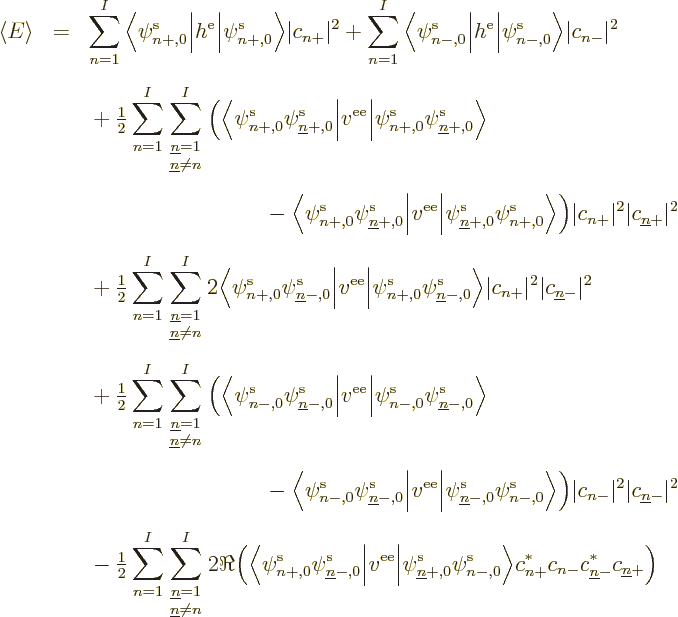
where  stands for the real part of its argument.
stands for the real part of its argument.
Now assume you have a normal unrestricted Hartree-Fock solution, and
you try to lower its ground-state energy by selecting, for example, a
spin-up orbital 

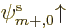 and adding some
amount of spin down to it. First note then that the final sum above
is zero, since at least one of
and adding some
amount of spin down to it. First note then that the final sum above
is zero, since at least one of 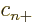 ,
, 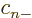 ,
,
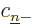 , and
, and 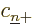 must be zero: all states except
must be zero: all states except  are still either spin-up or spin-down, and
are still either spin-up or spin-down, and  cannot be both
cannot be both  and
and
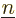
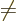
 . With the final sum gone, the energy is a
linear function of
. With the final sum gone, the energy is a
linear function of  , with
, with 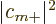

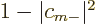 . The minimum energy must therefore occur for
either
. The minimum energy must therefore occur for
either 
 0, the original purely spin up orbital, or
for
0, the original purely spin up orbital, or
for 
 1. (The latter case means that the
unrestricted solution with the opposite spin for orbital
1. (The latter case means that the
unrestricted solution with the opposite spin for orbital  must have
less energy, so that the spin of orbital
must have
less energy, so that the spin of orbital  was incorrectly
selected.) It follows from this argument that for correctly selected
spin states, the energy cannot be lowered by replacing a single
orbital with a generalized one.
was incorrectly
selected.) It follows from this argument that for correctly selected
spin states, the energy cannot be lowered by replacing a single
orbital with a generalized one.
Also note that for small changes,  is quadratically small
and can be ignored. So the variational condition of zero change in
energy is satisfied for all small changes in orbitals, even those that
change their spin states. In other words, the unrestricted solutions
are solutions to the full variational problem
is quadratically small
and can be ignored. So the variational condition of zero change in
energy is satisfied for all small changes in orbitals, even those that
change their spin states. In other words, the unrestricted solutions
are solutions to the full variational problem
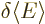
 0 for generalized orbitals as well.
0 for generalized orbitals as well.
Since these simple arguments do not cover finite changes in the spin
state of more than one orbital, they do not seem to exclude the
possibility that there might be additional solutions in which two or
more orbitals are of mixed spin. But since either way the error in
Hartree-Fock would be finite, there may not be much justification for
dealing with the messy problem of generalized orbitals with dubious
hopes of improvement. Procedures already exist that guarantee
improvements on standard Hartree-Fock results.

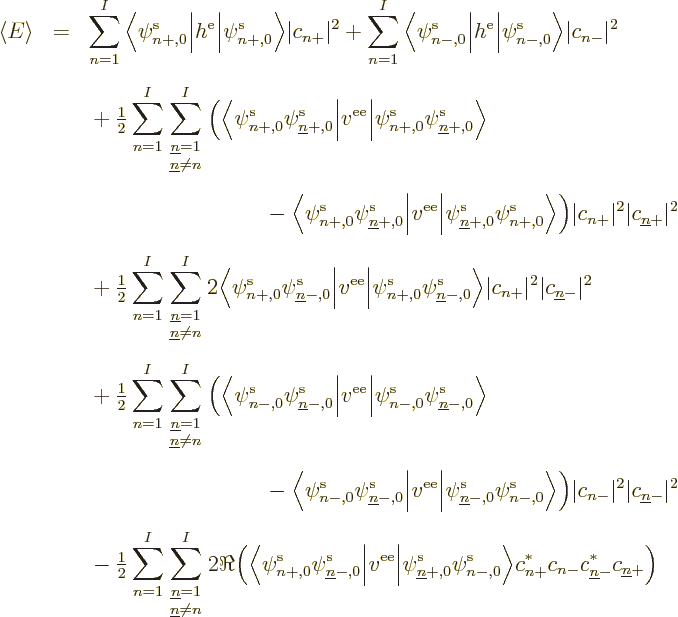
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()