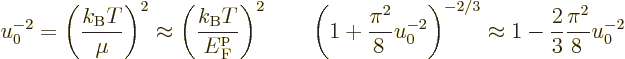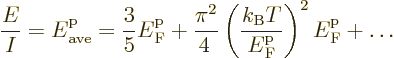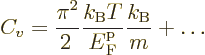| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.62 Fermi-Dirac integrals at low temperature
This note finds the basic Fermi-Dirac integrals for the free-electron
gas at low temperature. To summarize the main text, the number of
particles and total energy per unit volume are to be found from
where the Fermi-Dirac distribution and the density of states are:
and the number of spin states 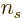

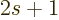
 2 for systems
of electrons. This may be rewritten in terms of the scaled energies
2 for systems
of electrons. This may be rewritten in terms of the scaled energies
to give
To find the number of particles per unit volume for small but nonzero
temperature, in the final integral change integration variable to 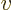

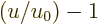 , then take the integral apart as
, then take the integral apart as
and clean it up, by dividing top and bottom of the center integral by
the exponential and then inverting the sign of 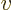 in the integral, to
give
in the integral, to
give
In the second integral, the range that is not killed off by the
exponential in the bottom is very small for large 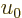 and you can
therefore approximate
and you can
therefore approximate  as
as 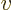 , or using a
Taylor series if still higher precision is required. (Note that the
Taylor series only includes odd terms. That makes the final
expansions proceed in powers of 1/
, or using a
Taylor series if still higher precision is required. (Note that the
Taylor series only includes odd terms. That makes the final
expansions proceed in powers of 1/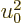 .) The range of
integration can be extended to infinity, since the exponential in the
bottom is exponentially large beyond
.) The range of
integration can be extended to infinity, since the exponential in the
bottom is exponentially large beyond 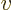
 1. For the same
reason, the third integral can be ignored completely. Note that
1. For the same
reason, the third integral can be ignored completely. Note that
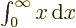

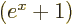

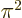
 12, see [41, 18.81-82, p. 132] for this and additional
integrals.
12, see [41, 18.81-82, p. 132] for this and additional
integrals.
Finding the number of particles per unit volume 

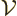 this way and
then solving the expression for the Fermi level
this way and
then solving the expression for the Fermi level  gives
gives
 |
(D.39) |
This used the approximations that 
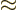
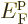 and
and
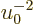 is small, so
is small, so
The integral in the expression for the total energy per unit volume
goes exactly the same way. That gives the average energy per particle
as
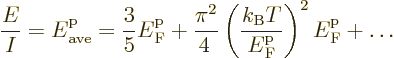 |
(D.40) |
To get the specific heat at constant volume, divide by  and
differentiate with respect to temperature:
and
differentiate with respect to temperature:
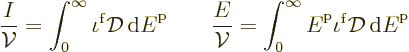
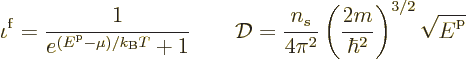
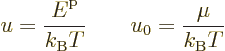
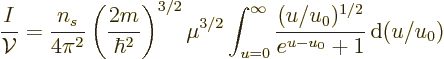
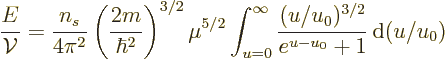
![]()
![]()
![]() ,
,
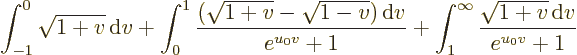
![]()
![]()
![]()
![]()